Вопрос по теории вероятностей

[confabulez]

Добрый день.
В курсе теории вероятностей, кажется, была теорема, в которой утверждалось, что если в игру с вероятностью выигрыша 1/2 играют два игрока со сколь угодно большим капиталом (делаяя ставку), то за конечное время кто-нибудь проиграет весь капитал. Можете подсказать ссылку на этот факт.

[TOTAL]

confabulez в сообщении #1189054 писал(а):

Добрый день.
В курсе теории вероятностей, кажется, была теорема, в которой утверждалось, что если в игру с вероятностью выигрыша 1/2 играют два игрока со сколь угодно большим капиталом (делаяя ставку), то за конечное время кто-нибудь проиграет весь капитал. Можете подсказать ссылку на этот факт.

Это не факт. В условии надо уточнять, какие ставки они делают.

[confabulez]

Т.е. допустим у каждого есть по 1 млн. рублей и они делают ставку по 1 рублю на каждый кон. В этом случае утверждение неверно и игра может никогда не закончиться?

[Sinoid]

А вообще в "Курс теории вероятностей" Гнеденко это рассматривается.

[TOTAL]

confabulez в сообщении #1189056 писал(а):

Т.е. допустим у каждого есть по 1 млн. рублей и они делают ставку по 1 рублю на каждый кон. В этом случае утверждение неверно и игра может никогда не закончиться?

Утверждение верно. Оно очевидно. (Представьте себе индукцию по количеству денег в кармане.)

А вот если бы они делали, скажем, уменьшающиеся (в два раза) ставки, то не закончится.

[Someone]

В учебнике А. А. Боровкова "Теория вероятностей" задача о разорении в безобидной игре рассматривается в конце § 2 главы 4 для случая, когда капитал одного из игроков бесконечен. Показано, что игрок с конечным капиталом разоряется за конечное время с вероятностью $1$, но средняя продолжительность игры бесконечна (собственно, ради этого задача и рассматривается: показать пример случайной величины, не имеющей математического ожидания).

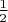
Если начальные капиталы обоих игроков конечные (обозначим их $m_1$ и $m_2$ единиц), ставка в каждой игре равна одной единице, а вероятности выигрыша и проигрыша равны $\frac 12$, то вероятности разорения игроков равны, соответственно, $\frac{m_2}{m_1+m_2}$ и $\frac{m_1}{m_1+m_2}$, а средняя продолжительность игры — $m_1m_2$. Вероятность разорения больше у того игрока, у которого капитал меньше.

А вообще, поиск в Интернете даёт массу ссылок на задачу о разорении.

[confabulez]

Спасибо.