
и

, насколько понимаю, свободные в том месте.
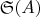
— группа перестановок элементов

.
-- Вт апр 05, 2016 03:49:23 --(Там именно
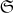
, как написали вы, и не
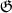
, как написано у
bin.)
Ещё забыто
вторая версия статьи писал(а):
Definition 2.4.8. Let
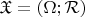
be a relational structure. We say that
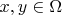
are strong twins for
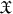
if they are strong twins for
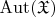
. We analogously transfer all concepts introduced in this section from groups to structures via their automorphism groups (weak twins, strongly/weakly symmetrical sets, symmetry defect). For instance, the (relative) symmetry defect of
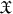
is the (relative) symmetry defect of
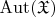
.
т. к. (двудольный) граф явно понимается как relational structure (пока не дочитал до Observation 7.2.2, но тут и гадать не следует).
[В цитате выше я где-то, видимо, забыл проставить курсив. Уже закрыл статью.]
-- Вт апр 05, 2016 04:03:31 --Далее (это пересказ 7.2 с начала), в двудольных графах
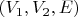
доли маркированы (первая и вторая), и изоморфизмы (стало быть, и автоморфизмы) не отображают вершины первой доли одного графа в вершины второй, и наоборот. При рассмотрении colored двудольных графов
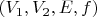
, где
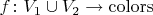
,
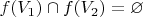
; изоморфизмы, конечно, сохраняют цвета.
Ещё:
вторая версия статьи писал(а):
Definition 7.2.1. Let
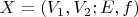
be a colored bipartite graph. We say that vertices
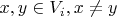
are
twins if they have the same color (in particular, they belong to the same part) and they have the same neighborhood:
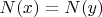
. For a subset
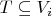
we use the phrase
“all vertices in  are twins”
are twins” to mean that all pairs of distinct vertices in

are twins.
чего как раз не хватало, потому что в Observation 7.2.2 три пункта.
Про окрестность искать не буду, моей помощи
bin уже достаточно.




