Очень Сложный многочлен на олимпиаде

[Grisha Landau]

Всех приветствую,у меня возник следующий вопрос,например у нас задача олимпиадная: Разложить многочлен на произведение многочленов,но приходит сразу в голову деление многочлена в столбик,но вдруг у нас не найдётся такого целого $\alpha$ - корня многочлена,как найти корень и разложить его на многочлена меньших степеней?Следующая идея приходит в голову,начать преобразовывать его,при помощи обычных формул,НО мы же понимаем что многочлен может быть очень сложный,как действовать в таких ситуациях?При этом задача должна решиться за 45 мин.

[miflin]

(Оффтоп)

Grisha Landau в сообщении #1185901 писал(а):

как действовать в таких ситуациях?

Отказаться от участия в олимпиаде.

[wrest]

Grisha Landau
См. презентацию "Многочлены. Решение олимпиадных задач по теме «Многочлены» Выполнила ученица 10 класса Б МБОУ лицея 1 Пщегорская Наталья. " здесь: http://www.myshared.ru/slide/394113/

[DeBill]

Grisha Landau в сообщении #1185901 писал(а):

При этом задача должна решиться за 45 мин.

Чтобы на олимпиаде задача такого сорта решилась за 45 мин, надо дома прорешать штук двадцать-сорок задач на эту тему - и не однотипных, а на самые разные методы. Обычно, это помогает....

(Оффтоп)

В свое время, будучи учеником седьмого класса, я обнаружил в книжке "Для поступающих ..." - у старшей сестры - задачку " Разложить на множители $x^4 +x^2 +1$". Уж как я над ней парился.... А задачка то оказалась простая - ну, после того, как я решение поглядел.... Так что - вот Вам один из рецептов - очень и очень специфический, кнешно - называется "представить в виде разности квадратов"

[TOTAL]

(Оффтоп)

DeBill в сообщении #1186004 писал(а):

Разложить на множители $x^4 +x^2 +1$". Уж как я над ней парился.... А задачка то оказалась простая - ну, после того, как я решение поглядел.... Так что - вот Вам один из рецептов - очень и очень специфический, кнешно - называется "представить в виде разности квадратов"

Для этой задачи подойдет и другой "специфический" прием: надо не разлагать на множители, а сделать совсем наоборот.

[Sender]

(Оффтоп)

Мне на эту тему вспоминается другая задача: доказать, что число $n^4+4$ составное при натуральных $n>1$. А что касается представления в виде разности квадратов, не так уж этот приём и специфичен, по-моему, школьная формула для корней квадратного уравнения выводится обычно именно с его помощью.

[DeBill]

Sender в сообщении #1186042 писал(а):

школьная формула для корней квадратного уравнения выводится обычно именно с его помощью.

Э, нет: школьная формула - из "выделения полного квадрата". Оно, конечно, и тут тоже "выделение". Но я - при работе с детьми/студентами - "выделение" резервирую именно что для "выделения" - потому как оно чаще по жизни встречается и нужно.

-- 20.01.2017, 13:02 --

(Оффтоп)

И - да, второй многочлен был блин в том же задачнике - и с тем же успехом...

[Brukvalub]

Интересно, а может ли кто-либо привести реальный пример "очень сложного многочлена на олимпиаде"? Мне, например, такие не попадались. Ведь олимпиады по математике - это соревнования на умение находить красивые решения трудных, неожиданных задач, изобретать новые способы рассуждений, а не на скорость разложения огромных многочленов на множители.
Для ТС: если не уметь мгновенно разложить на множители уже обсуждавшиеся в этой теме многочлены, то на олимпиаде делать нечего, все это тривиальные упражнения, а вовсе не "очень сложные многочлены на олимпиаде".

[Cash]

Самый сложный пример, что я встречал в школе - $x^{10}+x^5+1$

Идея о том, что давайте перед разложением это на что-нибудь умножим - одна из самых потрясных штук в математике.

[Sender]

Кстати, а как принято действовать, если требуется разложить на множители что-то вроде $x^4-x^3y+x^3-2x^2y+2xy^2+xy-2y^2$?
(Ничего не могу сказать про сложность этого конкретного примера, т.к. сам его только что придумал, но что-то похожее когда-то в школе поставило меня в тупик, притом задача была отнюдь не олимпиадная).

[Brukvalub]

Эта бяка квадратична по одной из переменных, так что нужно начать с дискриминанта.
Вот в этой статье рассмотрено несколько разных методов факторизации.

[Sender]

Спасибо. Действительно, идея дискриминанта лежит на поверхности. Я всё ещё не теряю надежды найти оригинальную задачу. Было стойкое ощущение, что она из сборника задач по алгебре за 8-9 классы Галицкого, но там ничего похожего не нашлось.

[wrest]

Sender в сообщении #1186086 писал(а):

$x^4-x^3y+x^3-2x^2y+2xy^2+xy-2y^2$

Я бы рассуждал по рабоче-крестьянски как-то так:
Попробуем разложить на два множителя. Поскольку у игреков максимальная степень двойка, а также поскольку есть игреки без иксов, значит игреки входят в оба множителя в степени не выше первой.
Свободных коэффициентов во множителях нет, иначе в произведении были бы квадраты иксов без игреков (если свободный коэффициент только в одном множителе) либо был бы свободный член в произведении (если свободные члены есть в обоих множителях).
Поскольку третья степень икса без игрека а свободных членов в множителях нет, значит в множители входят квадраты иксов (в множителях нет куба икса).


Так что будем искать разложение в виде
$(x^2+ax+bxy+cy)(x^2+dx+exy+fy)$ и значит, надо найти неизвестные коэффициенты $abcdef$
Видим, что $be=0$ поскольку в исходном многочлене нет члена $x^2y^2$
Произвольно полагаем $b=0$ и из коэффициента при $x^3y$ равному $-1$ сразу получаем $b+e=-1$ и следовательно $e=-1$. Осталось найти 4 коэффициента.
Из того, что коэффициент при $xy^2$ равен $2$, заключаем что $bf+ce=2$ а так как $b=0$ и $e=-1$ то $c=-2$ и осталось найти 3 коэффициента.
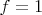
Из коэффициента при $y^2$ равного $-2$ находим что $cf=-2$ а поскольку $c=-2$, то $f=1$ и осталось найти два коэффициента -- $a$ и $d$.
Из коэффициента при $x^2y$ равного $-2$ находим что $f+c+bd+ae=-2$, подставляем ранее найденные коэффициента и получаем $1+(-2)+d\cdot 0+a\cdot (-1)=-2$ находим $a=1$
И, наконец, поскольку коэффициент при $x^3$ равен $1$, то $a+d=1$ и следовательно $d=0$
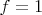
Итого, подставляем $a=1$;$b=0$;$c=-2$;$d=0$;$e=-1$;$f=1$ в $(x^2+ax+bxy+cy)(x^2+dx+exy+fy)$ и получаем ответ:

$x^4-x^3y+x^3-2x^2y+2xy^2+xy-2y^2=(x^2+x-2y)(x^2-xy+y)$

Вероятно это называют "метод неопределенных коэффициентов", не уверен.

[Someone]

wrest в сообщении #1186138 писал(а):

Вероятно это называют "метод неопределенных коэффициентов", не уверен.

Да, так и называют.

[TOTAL]

Cash в сообщении #1186084 писал(а):

Самый сложный пример, что я встречал в школе - $x^{10}+x^5+1$
Идея о том, что давайте перед разложением это на что-нибудь умножим - одна из самых потрясных штук в математике.

Просто без умножения
$(x^{10}-x)+(x^5-x^2)+(1+x+x^2)$