Привет всем! Нужно найти связь операторов рождения и уничтожения фононов для двухатомной цепочки с операторами координат атомов и импульсов. Для одноатомной цепочки это делается просто, выполняем преобразование Фурье для гамильтониана, потом вводим операторы рождения и уничтожения таким образом чтобы гамильтониан принял форму

В случае двухатомной цепочки попытался сделать то же самое. После преобразования Фурье


гамильтониан

(

и
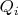
соответственно импульс первого и второго атома в

-ой ячейке) приобретает вид

(

-расстояние между ячейками)Теперь нужно ввести новые переменные чтобы гамильтониан стал диагональным. Если мы посмотрим на импульсную часть, то видим что она представляет с собой эллипс, а координатная часть - повернутый на некоторый угол эллипс. Последовательность действий такая: сначала ввожу новые координаты т.о. чтобы импульсная часть перешла в окружность (при этом координатная часть опять будет описываться повернутым эллипс), потом поворачиваю систему координат таким образом, чтобы оси эллипса были направлены вдоль координатных осей. Окружность при этом останется окружностью , а диагональный член в координатной части исчезнет. Т.о. получается диагональный гамильтониан - сумма двух гамильтонианов гармонических осцилляторов. Но частоты которые сидят в полученных выражениях не совпадают с акустическими и оптическими частотами для двухатомной цепочки. Никак не могу понять где я ошибся. В литературе тоже ничего не нашел, везде решается классические уравнения, потом по аналогии (без решения) с одноатомным случаем вводятся операторы рождения и уничтожения, но явный вид их через операторы координат и импульсов не приводится.