Масса в пылевидном решении (ОТО).

[Munin]

Вас обозначение сбивает. Просто подумайте, что такое стоит под интегралом.

[schekn]

Erleker в сообщении #1181234 писал(а):

Что и как?Надо же, чтобы смысл был, чтобы полученной по каким-то соображением именно с $r_{g}$ отождествлялось.

Вы проинтегрировали плотность вещества в собственной системе отсчета (103.11) из ЛЛ-2 и получили: $F(R_0)-F(0)=2MG/c^2$
Что вас смущает? $M$- масса частиц-пылинок.

Я понял, что вас смущает. Вам надо перейти от синхронной системы координат в шварцшильдовскую. Это сделано у Оппенгеймера-Снайдера, но там запутаетесь.
Лучше у Вайнберга на стр. 372. Далее сшиваются все 4 компоненты метрики с вакуумной метрикой Шварцшильда на границе вещества.

[Erleker]

Да, получили мы подобное выражение.

schekn в сообщении #1181237 писал(а):

Что вас смущает? $M$- масса частиц-пылинок.

Объясните, почему это так.Почему этот интеграл $M$ должен быть отождествлен с гравитационной массой?

schekn в сообщении #1181237 писал(а):

Вам надо перейти от синхронной системы координат в шварцшильдовскую. Это сделано у Оппенгеймера-Снайдера, но там запутаетесь.
Лучше у Вайнберга на стр. 372. Далее сшиваются все 4 компоненты метрики с вакуумной метрикой Шварцшильда на границе вещества.

Спасибо, посмотрю.

[schekn]

Erleker в сообщении #1181258 писал(а):

Спасибо, посмотрю.

Подумал, что можно еще проще. В рамках ЛЛ-2 по формуле (103.11) плотность обращается в ноль, когда $F=\operatorname{const}=F(R_0)$
То есть получаете вакуумное решение в синхронных координатах. Можете положить для простоты $f(R)=0$. А далее перейти к стандартным координатам Шварцшильда и найти постоянную $F(R_0)$.

[Erleker]

Можно вообще проще, если считать гравитационную массу аддитивной.
Вообще я понял, как можно сразу получить это решение с физическим смыслом, считая что внешняя пыль не действует.
Из З.С.Э ($mc^2\sqrt{1-r_{g}/r}/\sqrt{1-v^2/c^2}=E= \operatorname{const} $) находим локальную скорость изменения $r$ по собственному времени частицы $T$:
$(\frac{dr}{cdT})^2=\dfrac{v^2(1-r_{g}/r)}{c^2(1-v^2/c^2)}=((E/mc^2)^2-1)+r_{g}/r$
Каждой частице дадим метку $R$ (Это какая-то функция от радиуса $r_{1}$, на котором частица находится в некоторый фиксированный момент времени $T$).
Ищем метрику в координатах $R,T$:
Ясно, что $g_{00}=1$ и перед углами множитель $r(T,R)$.
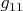
$g_{11}$ можно быстро найти, зная что это слагаемое - интервал между одновременными событиями $dT=0$ на 2-х частицах.
Тогда этот интервал есть собственная длина:
$dl=\sqrt{1-v^2/c^2}dr/\sqrt{1-r_{g}(R)/r}=\sqrt{g_{11}}dR$
Или, обобщая ($(dT=0)$):
$\sqrt{1-v^2/c^2}\dfrac{\partial r(T,R)}{\partial R}dR/\sqrt{1-r_{g}(R)/r}=\sqrt{g_{11}}dR$
Откуда:
$g_{11}=\dfrac{\partial r(T,R)}{\partial R}/(E/mc^2)^2$
Принимаем по определению $F(R)=r_{g}(R)$ - гравитационный радиус в-ва под данным слоем.
$f(R)=(E/mc^2)^2-1$ - функция от удельной энергии слоя пыли/ "разброс" скоростей.
И приходим к:
$ds^2=c^2dT^2-\dfrac{(\dfrac{\partial r(T,R)}{\partial R})^2}{1+f(R)}dR^2-r^2(T,R)(d\theta^2+\sin^2(\theta)d\varphi^2)$
$(\dfrac{\partial r(T,R)}{\partial T})^2=f(R)+\frac{F(R)}{r}$
Так как в центре шара у нас $F=0$, то общая гравитационная масса у нас $r_{g}=F(R_0)$ - на границе.

-- 02.01.2017, 20:06 --

Странно, что нигде в учебниках не был дан физический смысл этих функций, что $f$ это $(E/mc^2)^2-1$, хотя НФ на ее связь с энергией косвенно указывали.

-- 02.01.2017, 20:16 --

schekn,и согласитесь, что в ЛЛ-2 в 103 эта формула было получена как-то неверно, поскольку плотность же в координатах $R$,$T$.Эта какая-то "подгонка" под ответ:

[Munin]

Erleker в сообщении #1181465 писал(а):

Странно, что нигде в учебниках не был дан физический смысл этих функций

Странно, везде был дан...

Erleker в сообщении #1181465 писал(а):

поскольку плотность же в координатах $R$,$T$

Вот заладили! Да она одним множителем (присутствующим в формуле!) отличается от бескоординатной!

[Erleker]

Munin в сообщении #1181580 писал(а):

Erleker в сообщении #1181465 писал(а):

Странно, что нигде в учебниках не был дан физический смысл этих функций

Странно, везде был дан...

Я про то, что $f(R)=(E/mc^2)^2-1$.Разве это где-то есть?

Munin в сообщении #1181580 писал(а):

Вот заладили! Да она одним множителем (присутствующим в формуле!) отличается от бескоординатной!

Объясните.

-- 03.01.2017, 13:39 --

Правая часть после равенства верная, а левая (где интегрируется по $r$) из 100-го - там не к месту, они не равны(это ошибка, потому что в одном интеграле подразумевается $dt=0$, а в другом $dT=0$, а это существенно, поскольку у нас пыль эволюционирует).
Можно было из уравнений поля по таким же соображением(как 100-м для Шварцшильда) заново получить эту формулу уже для этого решения.

[Munin]

Erleker в сообщении #1181642 писал(а):

Я про то, что $f(R)=(E/mc^2)^2-1$.Разве это где-то есть?

Зачем писать банальность, если её в другом виде уже написали?

Erleker в сообщении #1181642 писал(а):

Объясните.

Когда вы начнёте интегрировать?

[Erleker]

Munin в сообщении #1181667 писал(а):

Когда вы начнёте интегрировать?

Так я же уже убедился, почему это так.
$M=4\pi\int\limits_{0}^{R_{0}}r^2p\frac{\partial r}{\partial R}dR=c^2(F(R_{0})-F(0))/2G=c^2F(R_{0})/2G$ - это ясно.
Но это выражение не равно:
$4\pi\int\limits_{0}^{r}pr^2dr$

[Munin]

Во-первых, плотность набирается буквой $\rho.$

Во-вторых, $\dfrac{\partial r}{\partial R}dR=dr.$

[Erleker]

Нет, в общем случае $\dfrac{\partial r}{\partial R}dR+\dfrac{\partial r}{\partial T}dT=dr.$Одновременность разная вообще-то и это существенно.Первый интеграл одновременен по $t$.Посмотрите его вывод в 100-м.
Да и центр шара необязательно в $r=0$.

[Munin]

Erleker в сообщении #1181869 писал(а):

Нет, в общем случае $\dfrac{\partial r}{\partial R}dR+\dfrac{\partial r}{\partial T}dT=dr.$

А в данном частном?

Erleker в сообщении #1181869 писал(а):

Да и центр шара необязательно в $r=0$.

А в данном частном случае?

[Erleker]

Ну так они же не написали $r(R,T)$, а использовали формулу из 100, где интеграл берется по $dt=0$ , а не $dT=0$.
И так это же решение для материи вообще, а центр шара может быть в другой $R$- области, не на $r=0$.

[Munin]

Erleker в сообщении #1182034 писал(а):

Ну так они же не написали $r(R,T)$

Они рассчитывали, что у читателя собственных мозгов хватит. В книгах такого уровня подобные мелочи обычно не разжёвываются. Подразумевается, что это для читателя не сложнее, чем дышать.

[Erleker]

Вы, похоже, совершенно не понимаете, о чем я...
Нет, ну я конечно понимаю, что я не очень умный, но не надо пожалуйста принимать меня за дурака!
Перечитайте мои сообщения и поймите, что я имел ввиду.

-- 05.01.2017, 16:57 --

Они написали согласно 100,23, значит они автоматически использует эту формулу, где по $r$ интеграл берется одновременно по $t$.То есть подразумевается $r(t,R)$ , а не $r(T,R)$.