И снова пресловутая сила натяжения нити...

[Neinstein]

Здравствуйте!

Казалось, что удалось-таки разобраться с направлением силы натяжения нити, да не тут-то было...

В определённых случаях направление силы натяжения вопросов не вызывает. Например, груз, подвешенный к невесомой нити.



Или же случай с грузом, перекинутым через блок.



В обоих случаях Земля притягивает тело к себе, а нить сопротивляется этому, т.е. сила натяжения нити направлена в противоположную притяжению сторону.

Но столкнулся с задачками с центростремительным ускорением. В одной из них действо происходит на наклонной плоскости, один конец нити жёстко фиксирован, а на другом её конце висит тело. Телу сообщают некоторую начальную скорость, вследствие чего оно начинает двигаться по окружности. Рисунок приведён ниже.



Интересуют меня направления сил в точках A и B. Мои рассуждения: сила тяжести всегда направлена перпендикулярно вниз, проекция в «плоскость действия» остальных сил равна $m \cdot g \cdot \sin \theta$, центростремительное ускорение — ускорение, которое старается тело приблизить к центру, т.е. можно представить, что нить при этом испытывает незначительное сжатие, т.е. сила натяжения нити направлена против ускорения.
Таким образом, в точке А имеем (за положительное принял направление в сторону подъёма по наклонной плоскости):

$-T-m \cdot g \cdot \sin \theta = m \cdot \frac{v^2}{R}$

В точке B проекция силы тяжести и центростремительное ускорение сонаправлены, сила натяжения направлена в противоположную сторону:

$T-m \cdot g \cdot \sin \theta = -m \cdot \frac{v^2}{R}$

Точку А сверить не с чем, а вот для точки B в решении приведена следующая диаграмма:



Почему сила натяжения направлена в итоге в другую сторону?

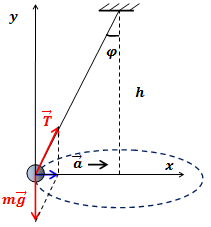
В другой задаче с центростремительным ускорением ситуация следующая: мяч массы $m$ подвешен на нити длины $l$, мячу сообщают такую скорость $v_0$, что он начинает двигаться по окружности. Нужно найти силу натяжения нити в вершине окружности, по которой мяч двигается.



Авторами приводится следующая диаграмма действующих в вершине окружности сил:



История та же самая, но почему сила натяжения сонаправлена с силой тяжести, я не понимаю... Ранее я воспринимал её, как силу сопротивления. Помогите разобраться, пожалуйста.

Заранее спасибо!

[DimaM]

Neinstein в сообщении #1179377 писал(а):

т.е. можно представить, что нить при этом испытывает незначительное сжатие

Возьмите нитку и начните ее сжимать. Что-то мне подсказывает, что без использования клея никакой силы сопротивления получить не удастся .
В задачах всегда нить может тянуть, но никогда не может толкать (в этом случае пишут про стержень).
Ваша ошибка, похоже, в том, что вы думаете, будто ускорение "влияет" на тело. На самом же деле ускорение - это результат действия сил. То есть второй закон Ньютона для тела постоянной массы нужно записывать в виде

$$m\mathbf a=\sum\mathbf F.$$

[Dragon27]

Силу натяжения нити обычно потому и называют натяжением, что она тянет, а не толкает

[wrest]

Если нить связывает лошадь и телегу, то с точи зрения лошади, сила натяжения нити направлена в сторону телеги, а с точки зрения телеги, сила натяжения нити направлена в сторону лошади.
А всё из-за третьего закона Ньютона...

[wide]

На столе лежит кубик, к нему привязана веревка. Вы тяните за веревку. Что при этом происходит? Вы являетесь "центром" и тем самым вызываете центростремительное ускорение у кубика. Теперь посмотрите как и к чему приложены силы. Мысленно разорвем веревку посередине. Вы увидите, что в месте разрыва на той части веревки, которая осталась с кубиком, сила приложена в вашу сторону, т.е. веревка натянута. Но в соответствии с 3 законом Ньютона на веревку, которая осталась в вашей руке, в месте разрыва, сила действует в обратном направлении, т.е. получается опять, что веревка в руке натянута. Теперь место разрыва можете сместить к самому кубику и сказать, что на кубик, со стороны веревки, сила действует в направлении на вас (что вызывает центростремительное ускорение кубика), а на веревку, со стороны кубика действует сила в направлении от вас, что и вызывает ее натяжение.

[DimaM]

wide в сообщении #1179400 писал(а):

На столе лежит кубик, к нему привязана веревка. Вы тяните за веревку. Что при этом происходит? Вы являетесь "центром" и тем самым вызываете центростремительное ускорение у кубика.

Какое еще "центростремительное ускорение" в этом случае?

[iifat]

Neinstein в сообщении #1179377 писал(а):

Почему сила натяжения направлена в итоге в другую сторону?

В какую такую другую? В сторону центра же на рисунке, нет?

[wrest]

DimaM в сообщении #1179403 писал(а):

Какое еще "центростремительное ускорение" в этом случае?

Если вы прилагаете силу к невесомой нерастяжимой веревке, то вы являетесь центром, в сторону которого направлена сила, которую прилагает второй конец веревки к телу, привязанному к веревке с другого от вас конца.

[DimaM]

wrest в сообщении #1179409 писал(а):

Если вы прилагаете силу к невесомой нерастяжимой веревке, то вы являетесь центром, в сторону которого направлена сила, которую прилагает второй конец веревки к телу, привязанному к веревке с другого от вас конца.

Эта лингвистика в какой-то мере занимательна, но все же традиционно понятие центростремительного ускорения определено по-другому.

[wrest]

DimaM в сообщении #1179414 писал(а):

Эта лингвистика в какой-то мере занимательна, но все же традиционно понятие центростремительного ускорения определено по-другому.

Да это Ньютон все запутал, это же он называл центральную силу центростремительной.
Но вы правы конечно, современное понимание термина -- другое.

[wide]

(Оффтоп)

DimaM в сообщении #1179403 писал(а):

Какое еще "центростремительное ускорение" в этом случае?

Недопонимание ТС, на мой взгляд, состоит в том, что он забывает про 3 закон Ньютона и не различает к каким телам какая сила приложена.
Согласен, в кавычках должен быть не только "центр", но и "центростремительное ускорение".
Приведенный анализ сил нужно применить к предоставленным задачам ТС, где движение по окружности присутствует в явном виде.

[rustot]

Есть кажущиеся сложными случаи, когда неочевидно как приложена сила нитью к телу, например тянут нить намотанную на катушку и сила приложена нитью к катушке в общем то во многих точках дуги а не в точке где нить сходит с катушки.

Но решается это очень просто, можно системой к которой приложена сила считать не "катушку" а "катушку плюс намотанная на нее нить плюс небольшой кусочек этой нити уже не касающийся катушки". И оказывается что вот к этой то системе сила оказывается приложенной именно в точке где соединены "нить" и "кусочек нити считаемый частью системы", а она может быть направлена только вдоль нити.

[Neinstein]

Всем огромное спасибо за отклики!

Правда, всё равно пока не дошло... И дело вроде не в 3-ем законе Ньютона. Пусть тело прикреплено к нити, верхний конец нити жёстко закреплён. Тогда на шарик со стороны Земли действует сила тяжести, а со стороны нити — сила натяжения, причём силы эти равны по модулю и противоположны по направлению, т.е. сила натяжения уравновешивает силу тяжести. А теперь случай с центростремительным ускорением. Что изменилось? Добавилось это самое ускорение, но сила тяжести снова стремится притянуть тело к Земле, а если у меня не будет силы, которая не сможет её скомпенсировать, нить просто порвётся, разве нет?

[DimaM]

Neinstein в сообщении #1179443 писал(а):

А теперь случай с центростремительным ускорением. Что изменилось? Добавилось это самое ускорение, но сила тяжести снова стремится притянуть тело к Земле, а если у меня не будет силы, которая не сможет её скомпенсировать, нить просто порвётся, разве нет?

Вы опять почему-то считаете ускорение причиной силы. На самом деле наоборот.

[Neinstein]

DimaM,
ммм... но об этом же гласит 2-ой закон Ньютона: если сумма всех действующих на тело сил отлична от нуля, то тело движется ускоренно.