Здравствуйте.
В
данной статье на стр. 637 приведено определение идеалов Галуа (определение 2.1).
Например, вот неприводимый многочлен

в
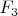
.
Я так понимаю можно рассмотреть

, где

. Тогда элементы расширения:

.
В таком расширении корнями многочлена будут

.
Но как теперь по этим корням построить идеал?
|
i |
Lia: Оформляйте ссылки. Исправлено. |