Hi,
I try to find my error in that device:

Blue color is small spheres like molecules of water attracted by springs to have the pressure like gravity can do on water. I noted the pressures inside the container. I noted in pink color the pressures from the pink springs. I noted in green color the pressures from the green springs. The springs attract blue spheres (blue color) from the green line or from the pink line. The area is constant. I drew in dotted line the device after a time. I drew one spring to show the direction of attraction. There is one spring for each blue sphere. I rotate left and right walls clockwise around their red dot. The walls are rigid. The green line moves in translation to the right. The length of the springs are changing. The orientation of the springs follow the orientation of the left (or right) wall. I noted some pressures 'p'. Walls are rigid, the area is constant,
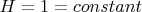
. Pink wall is fixed to the ground. Green wall moves in translation to the right.
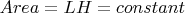
. If there is friction, that friction is an energy so it must be counted I lost a part of mechanical energy in friction but I win a heat, so I study that device without friction.
For a small angle of rotation

:
Energy needed for move the green line
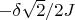
the force of attraction is 0.5N and the green line moves of
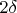
and the orientation of the force needs to divide by
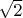
Energy won by the springs:
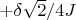
the bottom part win the same that the upper, one part win
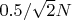
and the length increases from 0 to

, the mean is

so for one part it is

Energy won by walls in rotation:



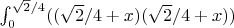
it is
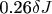
The sum of energy is:
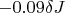
Could you help me to find my error ? I think the results of the energy needed for the green line and the length of springs are correct because when there is an horizontal wall at the middle of the device (between blue spheres attracted by pink springs and blue springs), I found the sum of energy at 0 because the pressure inside the blue shape are the pressures I noted in pink color and green color. So my error could become from the pressures of the calculation of the work to rotate the walls.
Don't hesitate if something is not clear.
Thanks



