offtop: Вот почему на mathoverflow всегда нормально отвечают, даже если ошибешься немножко.
А тут сразу воспитывать начинают? :((
Простите.
Вот на картинке правильный вариант.

Исходные окружности чёрные. Радикальная ось красная. Две выбранные на ней точки

и

не показаны, но их легко получить. Например,

— это пересечение касательной к верхней окружности в

и касательной к нижней окружности в

.
То, что

, и эти отрезки касательные, означает, что существует окружность, касающаяся двух исходных в точках

и

соответственно. Аналогично, существует окружность, касающаяся их в

и

. Эти две новые окружности зелёные.
Известно (Вики, статья Центр подобия), что любая окружность, касающаяся двух других окружностей, касается их в антигомологичных точках. Следовательно, центр гомотетии

зелёных окружностей лежит на пересечении
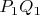
и
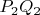
.
Вам остаётся понять (с помощью той же статьи), почему

лежит на радикальной оси исходных окружностей.