Ага.
У такого выбора есть достоинства (точное решение ограничено) и недостатки (из-за ошибок округления может возникнуть небольшая, но экспоненциально растущая примесь других собственных векторов, которая вскоре забьёт экспоненциально убывающее точное решение).
Вы, наверное, знаете, что собственные векторы определены с точностью до умножения на скаляр

. Если

, то

. Пользуясь этим, Ваш вектор можно упростить до

(проверьте, что этот вектор тоже подходит в качестве собственного для
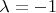
).
Остается вопрос про общую форму уравнения, к которой применим метод. Когда Вы её запишете, я скажу, где в этом выражении учитывается матрица.