Hello,
Inside the triangle (black+red at start) there is a gas under pressure P. I rotate with an external device two black arms around the black dot axis and I move up the red line in the same time to keep constant the area of the triangle. I drawn the triangle in gray color after an angle of
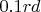
. There are gaskets between the black walls and the red: the gas don't escape. It is a theoretical device, I don't take in account the mass and the friction.
At start,
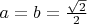
m and
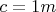
Gas under pressure

Area of the triangle =

= constant
Calculation for an angle of

Depth of the device =
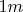
, the depth don't appear in the calculations
Energy from the black arms :I have the surface constant so I can write:
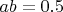
with a and b two sides of the triangle, so
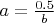
Pythagoreans' theorem:
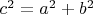
with a, b, c the sides of the triangle with
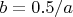
I have
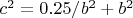
I have
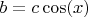
so I can write



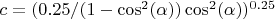
I have two arms but I need to divide by two for the moment so the energy is:
 Energy needed by the red line:
Energy needed by the red line:The area is constant, so the length of the red line is :
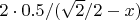
, so the energy is:
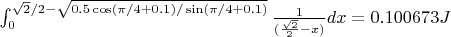
There is a small difference, I don't know if it is my integrals or the calculations.
I drawn the device:


Цитата:
You should add them together.
I thought the energy from the black arms must be the same than the red arm (the same in value), the sum of energy is not 0.100336-0.100673 ?
Цитата:
And it's nothing wrong with them being different
. If the volume is constant the gas don't lost/win any potential energy. I supposed the mass at 0 even for the gas, no friction, the gas keeps the same temperature, so where goes the difference of energy ?



