Задача формулируется таким образом:
Есть множество устройств

, которые должны передать свою информацию (i) контроллеру. Для этого выделено

слотов времени, в каждый из которых передать свою информацию может лишь одно устройство. В каждый слот времени мы сами выбираем, какую комбинацию i (т.е. от каких устройств) мы передаем. Если два и более устройства одновременно пытаются передать информацию в одном слоте, то информация считается потерянной. Если устройство передало свою информацию, то больше оно не активно, даже если в следующих слотах в расписании оно значится. Например, мы передаем в данном слоте

. Если

уже передало свою i, то

может передать свою. И наоборот, если

уже передало свою i, то

может передать свою. Если же в предыдущие слоты ни одно из устройств не передало свою информацию, то они могут пытаться передать одновременно и в этом случае вся информация от них теряется. Все вероятности перехода известны и не зависят от времени.
Нужно найти расписание (последовательность активных устройств в каждом слоте), чтобы после всех

слотов вероятность передачи информации со всех устройств

была бы максимальной
Задача решается перебором, но при больших размерностях очень долго. Предполагаю, что задача np-hard, но не знаю, как доказать.
Задачу можно свести к последовательности умножения матриц. Пусть

– это столбец вероятностей передачи информации после выполнения k слотов:
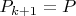
(передали

, передали только

, передали только

, передали только

,…, передали

),

Тогда

Где матрица

может принимать любое значение из множества размерности

. Это множество - есть множество матриц вероятностей перехода для любого возможного действия – расписания в данном слоте. Все эти матрицы - нижнетреугольные стохастические (сумма элементов любого столбца равна 1).
Нужно найти определить такую последовательность матриц, при перемножения которых, мы получим наибольшее значение в левом нижнем углу.
Есть ли у кого-нибудь идеи,
1) как доказать, что задача np hard
2) придумать какой-нибудь критерий выбора субоптимальной последовательности, которая даст решение близкое к оптимальному, но вычислительно не так затратно.



