vpb, спасибо. Что-то такое и хотелось сделать, но уже не было времени обдумать.
Это лишнее: норма есть функция вида

.
существуют ли нормы, отличные от норм такого вида (т.е., вида

)?
Интересный вопрос. Как мне видится, ответ будет положительным. Попробую показать на несложном примере. Для начала определим

, далее зафиксируем произвольное простое число
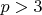
. Определим функцию
![$$N(2^nm)=\begin{cases}N_0(2^nm),&\text{если $m\neq p$;}\\ \left[\frac{p}2\right]_{ev}+1,&\text{если $m=p$,}\end{cases}$$ $$N(2^nm)=\begin{cases}N_0(2^nm),&\text{если $m\neq p$;}\\ \left[\frac{p}2\right]_{ev}+1,&\text{если $m=p$,}\end{cases}$$](https://dxdy-03.korotkov.co.uk/f/6/6/9/66948511a9023108592b3effa58c9a5782.png)
где
![$[x]_{ev}$ $[x]_{ev}$](https://dxdy-04.korotkov.co.uk/f/f/8/d/f8dc8ae5b559595a8cafa2171fcf740282.png)
— округление к ближайшему чётному. Таким образом норма останется прежней везде, кроме одной точки, являющейся простым числом (в этой точке значение «просядет» и будет равным минимальному нечётному большему половины

: например для

будет

, для

—

, для

—

). Покажем, что определённая функция есть норма, предварительно заметив, что

, ибо
![$$\left[\frac{p}2\right]_{ev}+1<\frac{p}2+2<\frac{p}2+\frac{p}2=p,$$ $$\left[\frac{p}2\right]_{ev}+1<\frac{p}2+2<\frac{p}2+\frac{p}2=p,$$](https://dxdy-04.korotkov.co.uk/f/f/f/e/ffeb2483a10edc45c0cd59d5746c5b3882.png)
так как
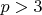
, а значит,

и

. В общем,

.
1.

. Таким образом, первое свойство доказано.
2. Будем делить

на

. Если

, то производим деление по тому же принципу, что и для нормы

. Таким образом мы получим пару чисел

. Если

, то, произведя деление «обычным» способом (как для

), мы получим три возможных исхода:
1)

— в этом случае оставим

и

;
2)
![$r=2^{n_r}m_r:|m_r|<\frac{p}2\Rightarrow|m_r|<\frac{p}2<\left[\frac{p}2\right]_{ev}+1\Rightarrow N(r)<N(b)$ $r=2^{n_r}m_r:|m_r|<\frac{p}2\Rightarrow|m_r|<\frac{p}2<\left[\frac{p}2\right]_{ev}+1\Rightarrow N(r)<N(b)$](https://dxdy-04.korotkov.co.uk/f/f/0/0/f0086e0ec478bcaa16d2586866f9a3d182.png)
, следовательно

и

подходят;
3)

— в этом случае возьмём



— округление «вверх» (к большему по модулю:

). Для начала стоит прояснить ситуацию. Например

. Можно поделить

на

двумя способами:

либо

. Первый способ, очевидно, не подходит, поэтому мы заменяем его вторым. Покажем, что

и

разных знаков, приняв, что

(случай, когда

будет аналогичен, но с противоположными знаками):
![$$\frac{m_1}{m_2}>0\Rightarrow\left[\frac{m_1}{m_2}\right]<\frac{m_1}{m_2}<\left\lceil\frac{m_1}{m_2}\right\rceil\Rightarrow m_2\left[\frac{m_1}{m_2}\right]-m_1<0<m_2\left\lceil\frac{m_1}{m_2}\right\rceil-m_1;$$ $$\frac{m_1}{m_2}>0\Rightarrow\left[\frac{m_1}{m_2}\right]<\frac{m_1}{m_2}<\left\lceil\frac{m_1}{m_2}\right\rceil\Rightarrow m_2\left[\frac{m_1}{m_2}\right]-m_1<0<m_2\left\lceil\frac{m_1}{m_2}\right\rceil-m_1;$$](https://dxdy-03.korotkov.co.uk/f/e/4/a/e4a86bdd0d4fdcbf2271e1c96addff4082.png)
![$$\frac{m_1}{m_2}<0\Rightarrow\left[\frac{m_1}{m_2}\right]>\frac{m_1}{m_2}>\left\lceil\frac{m_1}{m_2}\right\rceil\Rightarrow m_2\left[\frac{m_1}{m_2}\right]-m_1>0>m_2\left\lceil\frac{m_1}{m_2}\right\rceil-m_1.$$ $$\frac{m_1}{m_2}<0\Rightarrow\left[\frac{m_1}{m_2}\right]>\frac{m_1}{m_2}>\left\lceil\frac{m_1}{m_2}\right\rceil\Rightarrow m_2\left[\frac{m_1}{m_2}\right]-m_1>0>m_2\left\lceil\frac{m_1}{m_2}\right\rceil-m_1.$$](https://dxdy-04.korotkov.co.uk/f/b/2/9/b2932d5b6680aa0641402360f7c8070b82.png)
Далее, заметив, что

, если

:
![$$\frac{p}2+|m_{r'}|<|m_r|+|m_{r'}|=|m_r-m_{r'}|=\left|m_1-m_2\left[\frac{m_1}{m_2}\right]-m_1+m_2\left\lceil\frac{m_1}{m_2}\right\rceil\right|=|m_2|=p,$$ $$\frac{p}2+|m_{r'}|<|m_r|+|m_{r'}|=|m_r-m_{r'}|=\left|m_1-m_2\left[\frac{m_1}{m_2}\right]-m_1+m_2\left\lceil\frac{m_1}{m_2}\right\rceil\right|=|m_2|=p,$$](https://dxdy-03.korotkov.co.uk/f/a/3/9/a39b4bbdb7d3d86614055b3c3ee779f382.png)
ибо
![$|\lceil x\rceil-[x]|=1$ $|\lceil x\rceil-[x]|=1$](https://dxdy-02.korotkov.co.uk/f/5/d/1/5d1df12ff8280915b97e94bd426ac51782.png)
, если
![$x\neq[x]$ $x\neq[x]$](https://dxdy-01.korotkov.co.uk/f/4/5/3/453174e6a27dc2dff44a8fc3cc1fb5e282.png)
(в этом случае

). В итоге:
![$|m_{r'}|<\frac{p}2<\left[\frac{p}2\right]_{ev}+1\Rightarrow N(r')<N(b)$ $|m_{r'}|<\frac{p}2<\left[\frac{p}2\right]_{ev}+1\Rightarrow N(r')<N(b)$](https://dxdy-02.korotkov.co.uk/f/9/1/6/916a298c832edcf81b4ccc8308da569182.png)
. Таким образом мы получили подходящую пару

.
Результат:

— норма. Надеюсь, нигде не ошибся.
(Оффтоп)
Фух!
Думаю, что можно придумать ещё изощрённее примеры: функция, которая будет «проседать» во всех простых числах, а если число составное, то будет равна максимуму норм этих чисел с прибавлением единицы. Возможно, она тоже будет нормой, но проверять не очень хочется.



