Орбитальный магнитный момент

[ExtreMaLLlka]

Используя теорию Бора, определите орбитальный магнитный момент электрона с более высокого уровня энергии на более низкий уровень, если при этом энергия атома уменьшилась на 10 эВ.

Мое решение:
По теории Бора: $\Delta E=h\nu$, $\nu=\frac{\Delta E}{h}$
орбитальный магнитный момент: $p_m=IS$, $I=e\nu$.
Тогда, $p_m=e\frac{\Delta E}{h}S$.
Не понятно как найти S, радиус никакой не дан.

[Munin]

В такой постановке задача не имеет решения. Укажите все условия. Кроме того, уточните, где задача задана: школа (класс?), вуз (название курса? год, специальность - хорошо бы).

[ExtreMaLLlka]

задача вузовская, специальность далекая от физики

[Munin]

Остаётся вопрос по условиям.

-- 12.09.2016 11:59:14 --

У вас даже смысл обозначений не раскрыт.

-- 12.09.2016 12:06:06 --

У вас уже была проблема с физической задачей с какими-то невообразимо кошмарными условиями. Тут надо либо приводить полностью всю доступную информацию, вплоть до цвета обложки методички, либо заниматься гаданием, какие тараканы ползали в голове у автора задачи в тот момент, когда его прихватило вдохновение. Либо просто напрямую допрашивать автора.

[DimaM]

Думаю, имеется в виду следующее.
По Бору момент импульса (и связанный с ним орбитальный магнитный момент) равен $n\hbar$, где $n$ - номер уровня. При переходе с одного уровня на другой энергия меняется на известную величину, так что по разнице энергий можно найти номера начального и конечного уровня (10 эВ с точностью до двух знаков получается "между первой и второй").
Правда, что такое

ExtreMaLLlka в сообщении #1150689 писал(а):

орбитальный магнитный момент электрона с более высокого уровня энергии на более низкий уровень

лично я не понимаю. Хорошо бы увидеть вопрос задачи на нормальном, гражданском языке.

[Munin]

DimaM в сообщении #1150701 писал(а):

По Бору момент импульса (и связанный с ним орбитальный магнитный момент) равен $n\hbar$, где $n$ - номер уровня.

Вроде бы, уже в модели Бора выяснили, что момент импульса не равен $n\hbar,$ а находится в пределах от 0 до $n\hbar.$ По крайней мере, кажется, продвинутая модель Бора-Зоммерфельда имела все традиционные квантовые числа $n,l,m,s$ (спин могли добавить позднее).

Хотя это всё настолько неактуально для современной физики (модель Бора ушла в утиль 90 лет назад), что пускай этим историки науки занимаются, а для нормальных людей интереса не представляет.

DimaM в сообщении #1150701 писал(а):

10 эВ с точностью до двух знаков получается "между первой и второй"

Ага, если уточнить, что речь идёт о водороде. А если об ионизированном гелии? :-)

И я всё ещё не понимаю, что такое $I$ и $S.$

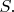
...Страшная догадка! Вдруг там не $I,$ а $l$ ???

-- 12.09.2016 12:44:26 --

Munin в сообщении #1150705 писал(а):

...Страшная догадка! Вдруг там не $I,$ а $l$ ???

ExtreMaLLlka, уточните, пожалуйста. И если это ваша неаккуратность, имейте в виду: в математике можно заменять буквы одни на другие (зафиксированы только несколько: $\pi,e,i,d,{\scriptstyle\int}$), а в физике нельзя. Каждая буква имеет заранее заданный и общеизвестный смысл.

[DimaM]

Munin в сообщении #1150705 писал(а):

И я всё ещё не понимаю, что такое $I$ и $S.$

...Страшная догадка! Вдруг там не $I,$ а $l$ ???

Решая обратную задачу, можно вычислить, что $I$ - это ток, $S$ - площадь орбиты (окружности). Классический магнитный диполь в виде колечка с током.

Munin в сообщении #1150705 писал(а):

Вроде бы, уже в модели Бора выяснили, что момент импульса не равен $n\hbar,$ а находится в пределах от 0 до $n\hbar.$

Вроде, до $(n-1)\hbar$, если нумеровать с единицы. Но это, по-моему, уже называют моделью Бора-Зоммерфельда, а в чистой модели Бора (которую некоторым школьникам преподают) именно $n\hbar$.

[Munin]

DimaM в сообщении #1150711 писал(а):

Решая обратную задачу, можно вычислить, что $I$ - это ток, $S$ - площадь орбиты (окружности). Классический магнитный диполь в виде колечка с током.

А! О! Задача постепенно приобретает смысл!

DimaM в сообщении #1150711 писал(а):

Вроде, до $(n-1)\hbar$

Точно, оговорился!

DimaM в сообщении #1150711 писал(а):

Но это, по-моему, уже называют моделью Бора-Зоммерфельда

У меня сложилось впечатление, что там было много версий этих теорий, ранние - под авторством Бора, более поздние - в соавторстве с Зоммерфельдом. Эллипсы, пространственные ориентации орбит - много ерунды было придумано.

Для меня, словосочетание Бор-Зоммерфельд скорее относится к правилу квантования $\oint p\,dq=2\pi\,n\hbar,$ которое было самым глубоким теоретическим обобщением до возникновения настоящей квантовой механики. И "отпутать" его от модели атома Бора-Зоммерфельда я не знаю как.

[ExtreMaLLlka]

Спасибо за ответы, буду узнавать более точную формулировку задачи.

[Munin]

DimaM в сообщении #1150701 писал(а):

При переходе с одного уровня на другой энергия меняется на известную величину

А вот момент - непонятно на какую.

Хотя из настоящей квантовой механики (точнее даже, из КЭД) мы знаем, что при переходе с излучением фотона происходит изменение момента на $\pm 1\hbar.$ Поэтому, например, если произошло излучение $2\to 1,$ то это $2p\to 1s.$

[Metford]

Munin в сообщении #1150705 писал(а):

По крайней мере, кажется, продвинутая модель Бора-Зоммерфельда имела все традиционные квантовые числа $n,l,m,s$ (спин могли добавить позднее).

Нет, спина там ещё не было. Статья "Zur Quantentheorie des Spektrallinien". В ней фигурирует формула для энергетического спектра с двумя квантовыми числами. Вот не помню, в этой ли статье или нет, но потом чисел стало три. Отталкивался Зоммерфельд от того, что сейчас адиабатическими инвариантами называется.

Если же возвращаться к задаче ТС, то она до боли напоминает что-то из задачника Савельева, только всё портит уже отмеченная выше фраза

ExtreMaLLlka в сообщении #1150689 писал(а):

орбитальный магнитный момент электрона с более высокого уровня энергии на более низкий уровень

которую я интерпретировать отказываюсь. Решается эта задача обычным способом, когда вполне в духе теории Бора движение электрона рассматривается как круговой ток с вычисляемым по простейшему варианту магнитным моментом, как отметил опять же DimaM. Но уточнений ТС всё же хотелось бы.

[Osmiy]

Metford в сообщении #1150788 писал(а):

Но уточнений ТС всё же хотелось бы.

Гуглиться на ура. Это 13 и 14 задачки из задачника/решебника Трофимова "Теория атома по Бору" http://studyport.ru/zadachi/fizika/trofimova/6895

Цитата:

13. Определите длину волны λ спектральной линии, излучаемой при переходе электрона с более высокого уровня энергии на более низкий уровень, если при этом энергия атома уменьшилась на ΔE = 10 эВ.
14. Используя теорию Бора, определите орбитальный магнитный момент электрона, движущегося по третьей орбите атома водорода.

[Munin]

Osmiy в сообщении #1157464 писал(а):

Гуглиться на ура.

"Гуглится" без мягкого знака.

А вообще дикость какая-то. Смешали две вменяемые задачки, и получили одну невменяемую.