Дифференцирование в Нейронные Сетях методе обратного распрос

[vladimircape]

У меня есть некоторые пробелы в понимании алгоритма, может кто поможет .
Там в итерационным цикле происходят некоторые вычисления.

Задача минимизировать суммарные потери
Суммарная потеря зависит от весов, входных данных, и выходных данных.
Минимизируем эту функциию потерь через метод численной оптимизации первого порядка градиентный метод.

Т.е чтобы минимизировать сумарные потери, надо н-ти производную функции потери
Я не много не понимаю почему именно производную

[dsge]

vladimircape в сообщении #1148165 писал(а):

Минимизируем эту функциию потерь через метод численной оптимизации первого порядка градиентный метод.
Т.е чтобы минимизировать сумарные потери, надо н-ти производную функции потери
Я не много не понимаю почему именно производную

Какое отношение градиент имеет к производной(ым)?
Про градиентный метод:
https://ru.wikipedia.org/wiki/%D0%93%D1%80%D0%B0%D0%B4%D0%B8%D0%B5%D0%BD%D1%82%D0%BD%D1%8B%D0%B5_%D0%BC%D0%B5%D1%82%D0%BE%D0%B4%D1%8B

[vladimircape]

dsge в сообщении #1148168 писал(а):

vladimircape в сообщении #1148165 писал(а):

Минимизируем эту функциию потерь через метод численной оптимизации первого порядка градиентный метод.
Т.е чтобы минимизировать сумарные потери, надо н-ти производную функции потери
Я не много не понимаю почему именно производную

Какое отношение градиент имеет к производной(ым)?
Про градиентный метод:
https://ru.wikipedia.org/wiki/%D0%93%D1%80%D0%B0%D0%B4%D0%B8%D0%B5%D0%BD%D1%82%D0%BD%D1%8B%D0%B5_%D0%BC%D0%B5%D1%82%D0%BE%D0%B4%D1%8B

Я уже разобрался, т.к. там где производная = 0 мы имеем максимум или минимум функции.

Но пока не могу понять почему так дифференцируется, а именно
возьмем эту фунцию стоимости
http://radikal.ru/big/47e1e25581c04140a9bbabd7bc8c3233
почему когда мы дифференцируем по например по w1 , появляется умножение на х1 в производной, т.е. 2 сокрашается от квадрата это понятно.

Вот более четкая картинка http://latex.codecogs.com/gif.latex?\frac{{\partial%20S}}{{\partial%20{{\hat%20b}_1}}}%20=%20\frac{\partial%20}{{\partial%20{{\hat%20b}_1}}}\sum\limits_{i%20=%201}^n%20{{{({y_i}%20-%20{{\hat%20b}_1}{x_{i1}}%20-%20{{\hat%20b}_2}{x_{i2}})}^2}%20=%20}%20\sum\limits_{i%20=%201}^n%20{2({y_i}%20-%20{{\hat%20b}_1}{x_{i1}}%20-%20{{\hat%20b}_2}{x_{i2}})(%20-%20{x_{i1}})%20=%200,}

я не понимаю почему выскочил в конце (-Хi1)

[dsge]

vladimircape в сообщении #1148453 писал(а):

почему когда мы дифференцируем по например по w1 , появляется умножение на х1 в производной

Как брать производную сложной функции?

[vladimircape]

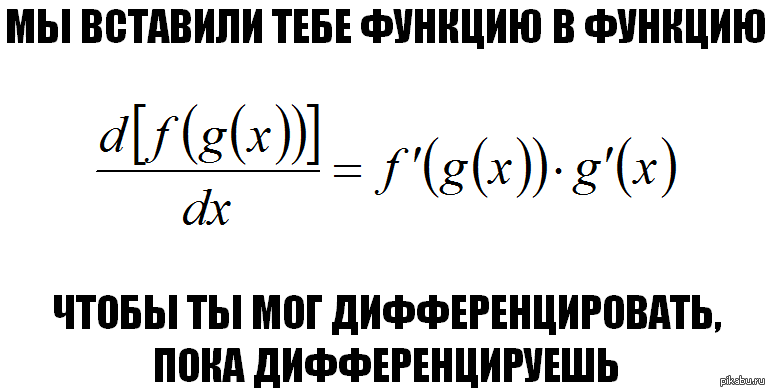
я не понимаю как выводится такое правило дифференцирование

-- 02.09.2016, 16:37 --

Меня больше интересует, не сами решения, а кто из математиков допёр до это формулы, какие проблемы он решал ,что пришлось применить и как вывел.

-- 02.09.2016, 16:55 --

Кажется нашёл

Лейбниц (1646-1716) ввёл символы и сформулировал
правила дифференцирования суммы, произведения и частного в 1675 году. Он
же сформулировал правило дифференцирования сложной функции