аналитичность в задаче Дирихле

[Gafield]

Из справочника Полянина Линейные уравнения математической физики.
Функция Грина первой краевой задачи в единичном круге:

$$ G(x,y)=\frac1{2\pi}\ln \frac1{|x-y|}-\frac1{2\pi}\ln \frac1{|y|\,|x-|y|^{-2}y|}. $$

[zoo]

спасибо конечно, у меня уверенности в том, что нельзя продолжить тоже поубавидлось, вначале я думал, что примеры такого сорта очевидны, оказывается все в этой задаче даже более непонятно, чем казалось

[Gafield]

Gafield писал(а):

Возможно, какое-нибудь аналогичное доказательство есть и для полигармонических .

Я тут прикинул, если $f$ полигармонична в круге $B_R$ радиуса $R>1$, то $u$ будет разлагаться в ряд, сходящийся также в $B_R$. В доказательстве используется тот факт, что в этом случае ряд для $f$ сходится в $B_R$. Думаю, отсюда можно как-нибудь получить требуемое для произвольной $f$, чей ряд Маклорена сходится в $B_R$. Это, конечно, более сильное условие, чем аналитичность $f$.

Однако расссмотрим радиально-симметричные решения. Пусть функция одного переменного $f$ разлагается в ряд Маклорена $f(x)=\sum_{k=0}^\infty{a_k x^k}$ в окрестности нуля и аналитична на отрезке $[-\varepsilon,1+\varepsilon]$ для некоторого $\varepsilon>0$. Тогда решение задачи с правой частью $f(r^2)$ также зависит только от $r^2=x^2+y^2$ и $u(r)=v(r)-v(1)$, где $v$ - аналитическое продолжение функции

$$v(r)=\sum_{k=1}^\infty{\frac{a_{k-1}}{4k^2} r^{2k}$$

на $(-\varepsilon,1+\varepsilon)$. Оно существует, поскольку единственное ограниченное в нуле решение получающегося ОДУ $u''(r)+u(r)/r=f(r^2)$ с условием $u(1)=0$ должно быть аналитическим на этом интервале. В частности, для функции $f(r^2)=(1+c^2 r^2)^{-1} $, выбирая $c$ большим, получим, что радиус сходимости $f$ может быть сколь угодно мал, особенность сколь угодно близка к нулю (в $\mathbb C^2$). 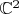А решение при этом аналитически продолжается туда же, куда и $f$.

Спрашивается, что же тогда может портить решение? По-моему, пора доказывать положительный ответ

Можно так. Из полученного решения для полигармонических функций вытекает, в частности, что утверждение верно для всех многочленов, поскольку они явл. полигарм. функциями. Более того, если $f$ - многочлен, то и $u$ многочлен. Поскольку в задаче (*) все производные начальных данных $\varphi_1$ и $\varphi_2$ оцениваются через $\sup_{B_R}|f(x)|<\infty$, то можно попытаться построить общее решение, приближая $f$ полиномами $f_n$. Пусть для задачи Коши есть какая-нибудь оценка, позволяющая получить оценку для $\sup_{B_{R_1}}|u|$, где $1<R_1<R$ через некоторые нормы $\varphi_1$ и $\varphi_2$ (которые оцениваются через $f$). Тогда, приближая $f$ полиномами в $B_{R_1}$ по норме $C$, можно было бы получить последовательность полиномов $u_n$, равномерно сходящуюся в $B_{R_1}$. Причем, если вычесть объемный потенциал для $f_n$, то оставшаяся разность $w_n$ будет гармонической ф. Поскольку посл. $\{w_n\}$ равномерно ограничена $C\sup_{B_R}|f|$, из этой последовательности можно выбрать подпоследовательность, равномерно сходящуюся в $B_{R_2}$, $1<R_2<R_1$ к некоторой гармонической функции $w$. Прибавить к ней о. п. $Vf$ и получится решение. Итого: осталось найти в литературе оценку для решений задачи Коши

[zoo]

вот все это вместе и то, что Вы радиальносим. решения расматриваете и функции полигармонические для меня означает, что шар не очень подходящее место:) для решения этой задачи, поэтому я иставил вопрос с самого начала о выборе адекватных областей. Например, хорошо задача о продолжении решений решается на компактном многообразии без края, хотя это немного о другом

[Gafield]

Имеются конформные отображения. Так что для односвязных областей в двумерном случае ответ практически исчерпывающий.

Использование полигармонических функций - прием, так сказать, "глобальный", позволивший найти решения явно. А продолжимость решений, вполне возможно, локальная храктеристика куска границы. Во всяком случае, это была бы обычная ситуация для эллиптических уравнений. Разве что какие-нибудь топологические препятствия для сложных областей появятся.

То, что доказательство впрямую не проходит для трехмерных областей еще не значит, что там нельзя общее решение приблизить какими-то простыми функциями. Вот интересно, продолжаются ли собственные функции задачи Дирихле? Их бы, возможно, хватило для доказательства в общей области.

Да и вообще непонятно, какой эффект мог бы отличать трехмерную область от двумерной в этом отношении.