Здравствуйте, я хотел бы еще раз поднять данную тему, т.к. тема для меня все еще актуальна
В прошлый раз закончилось обсуждение на том, что данную в задаче схему по теореме Тевенина привели для каждого положения ключа к данной схеме
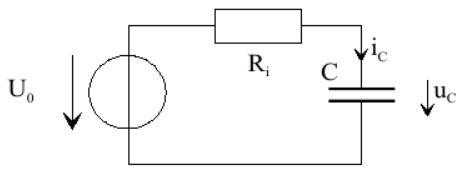
и нашли эквивалентное сопротивление

и напряжение

для каждого положения ключа
Где:
Ключ замкнут:

и

Ключ разомкнут:

и

В задании а) спрашивается: Какова величина напряжения

и тока

на конденсаторе в момент положения ключа в позиции 1, т.е. замкнутом?
Установили, что искомое напряжение

является найденным напряжением

, а

Теперь к заданию b) В монет

ключ разомкнули. Каково напряжение


? Каково напряжение


?
Если я правильно понимаю, то


, т.е. именно в момент времени

напряжение на конденсаторе остается таким же, каким оно и было до того, как ключ разомкнули, т.е.

. Т.е. именно в тот момент, как ключ переклюли напряжение еще старое, а потом уже с изменением времени напряжение на конденсаторе изменяется. Так ли это?
Тогда, например для момента

А для момента

Правильно ли я понимаю эти процессы?
-- 27.07.2016, 09:53 --И выглядит все это как-то так
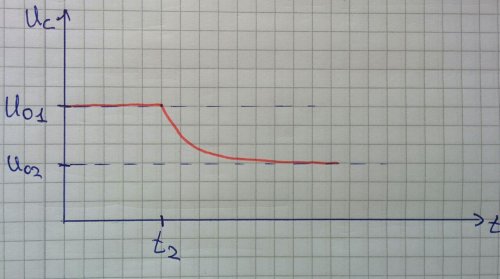
И тогда, как я и писал выше


Экспонента должна уходить в ноль, там, наверное, в числителе просто минус бесконечность должна стоять, тогда будет ноль и остается

В тему призывается
AnatolyBa :)



