Прошу участников форума проверить правильность моих решений и подсказать, как следовало сделать то, с чем я не справился.
Цитата:
Задача 1: Предположим, что группу можно представить в виде объединения двух подгрупп. Докажите, что одна из этих подгрупп совпадает со всей группой.
Решение:
Предположим, что допустимо такое представление, где ни одна из подгрупп не совпадает со всей группой. Пусть

и

-- две несовпадающие подгруппы, объединение которых есть группа

. Выберем

,

. Тогда

. Предположим, что

, тогда из

следует, что

, что неверно. Предположим, что

, тогда из

получаем, что

, что снова приводит к противоречию.
Цитата:
Задача 2: Найдите

, где

-- следующая перестановка:

Решение: Выпишем первые пять степеней заданной перестановки и обратим внимание, что
(а) элементы

переходят сами в себя при чётной степени и

при нечётной;
(б) элементы

переходят друг в друга внутри цикла в три перестановки, то есть для них

.
Тогда для

-й степени перестановки элементы

будут иметь те же образы, что и при

, а элементы

как при

.
В итоге

Цитата:
Задача 3: Сколько перестановок из

элементов могут быть представлены в виде произведения двух несовпадающих транспозиций?
Решение: Так как транспозиция меняет местами два элемента, то композиция двух несовпадающих транспозиций поменяет порядок трёх либо четырёх элементов. То есть на композицию двух транспозиций можно смотреть как на перестановку трёх или четырёх элементов. Всего на множестве из

элементов существует

перестановок, из них меняет местами три или четыре элемента:

.
Цитата:
Задача 4: Сколько автоморфизмов у группы

?
Решение: Пусть

-- изоморфизм групп. Из

следует, что единица переходит в единицу (

), а обратный элемент в обратный (

).
Автоморфизм -- это изоморфизм группы на себя.

-- аддитивная группа с единицей

, кроме того, каждый элемент в ней обратен самому себе. Значит всё возможные её автоморфизмы получаются перестановками элементов, отличных от единичного, друг с другом. Всего пять автоморфизмов, включая тождественный.
Цитата:
Задача 5: Найдите порядок группы

, где
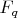
-- поле из

элементов.
К сожалению, продвинуться в решении этой задачи я не смог от слова совсем. По теме могу сказать только то, что порядок конечного поля всегда является степенью простого числа.
Цитата:
Задача 6: Верно ли, что поле из четырёх элементов изоморфно подполю поля из восьми элементов?
Решение: Удалось найти следующее утверждение: Поле

содержит в себе в качестве подполя

тогда и только тогда, когда

является делителем

. Доказательство этого факта не знаю, но выглядит похоже на следствие из теоремы Лагранжа для групп. В силу приведённого утверждения ответ на исходный вопрос отрицательный.
Цитата:
Задача 7: Найдите все обратимые элементы
(1) в кольце многочленов над полем

,
(2) в кольце целых гауссовых чисел.
Решение:
(1) Единичный многочлен -- это просто единица. Из того как устроено умножение многочленов получаем, что обратимы только многочлены, состоящие из одного лишь свободного члена (коэффициенты при остальных членах равны нулю), то есть комплексные числа.
(2) Пусть

и

некоторые гауссовы числа.

Единица имеет вид

. Для равенства произведения двух чисел единице получаем систему

решение которой имеет вид

то есть в кольце гауссовых чисел обратимы все числа с ненулевой реальной частью.
Цитата:
Задача 8: Является ли идеал в (a)
![$\mathbb{C}[x]$ $\mathbb{C}[x]$](https://dxdy-04.korotkov.co.uk/f/3/e/d/3ed9c49ea27a12adb4a8a8bbcdd647ac82.png)
, (b)
![$\mathbb{C}[[x]]$ $\mathbb{C}[[x]]$](https://dxdy-03.korotkov.co.uk/f/a/d/3/ad3f0a97bb6685f3c28e20e820897f1582.png)
, (c)
![$\mathbb{Z}[[x]]$ $\mathbb{Z}[[x]]$](https://dxdy-02.korotkov.co.uk/f/d/5/d/d5d0786401d2dffec2a2f1787480923582.png)
, порождённый элементом

, максимальным? Здесь
![$R[x]$ $R[x]$](https://dxdy-03.korotkov.co.uk/f/6/e/e/6ee92812dd8b4380e6b49feef2b5979182.png)
обозначает кольцо многочленов с коэффициентами в кольце

, а
![$R[[x]]$ $R[[x]]$](https://dxdy-03.korotkov.co.uk/f/e/5/2/e528feae4ba93a42de38cd8e13ffdf5282.png)
-- кольцо формальных степенных рядов над

.
Решение:
(a)
1.
![$\mathbb{C}[x]$ $\mathbb{C}[x]$](https://dxdy-04.korotkov.co.uk/f/3/e/d/3ed9c49ea27a12adb4a8a8bbcdd647ac82.png)
кольцо главных идеалов
2. идеал

максимален в кольце

тогда и только тогда, когда

поле
3.
![$P[x]/f(x)$ $P[x]/f(x)$](https://dxdy-02.korotkov.co.uk/f/5/0/e/50e4e776ca380a375fc0d3b15d731a7a82.png)
поле тогда и только тогда, когда

неприводим над

Так как

неприводим над

, то идеал, порождённый им, максимальный.
(b)
1. Если

локальное кольцо, то
![$R[[x]]$ $R[[x]]$](https://dxdy-03.korotkov.co.uk/f/e/5/2/e528feae4ba93a42de38cd8e13ffdf5282.png)
также локальное кольцо.
2. В любом поле нет нетривиальных идеалов, следовательно поле есть локальное кольцо.
По определению локального кольца имеем единственный максимальный идеал в
![$\mathbb{C}[[x]]$ $\mathbb{C}[[x]]$](https://dxdy-03.korotkov.co.uk/f/a/d/3/ad3f0a97bb6685f3c28e20e820897f1582.png)
.
(c) Не смог справиться.
Цитата:
Задача 9: Пусть
![$R = \mathbb{Z}[\sqrt d]$ $R = \mathbb{Z}[\sqrt d]$](https://dxdy-04.korotkov.co.uk/f/f/a/3/fa3b00f33356e73c48020d1539affd8182.png)
, где

-- целое число, не являющееся полным квадратом. Докажите, что

не является простым элементом в

(т.е. неверно, что если

делится на

, то либо

, либо

делится на

), однако, при

, этот элемент неприводим в

(т.е. если

, то либо

, либо

обратим).
Доказать не смог. Если

, то очевидным образом предъявляем

, но

. Как доказывать при других

непонятно. Мне даже кажется, что это неправда, потому что в


простой элемент, а если в произведении

ни один из множителей не

(

непонятно как использовать), то они из

.
Цитата:
Задача 10: Докажите, что многочлен

неприводим над целыми числами.
Решение: Нашёл корни по формуле Кардано и убедился, что они не целые числа. Но эта задача экзаменационная и должна подразумевать решение без ЭВМ и калькулятора, а тут коэффициенты к этому не располагают (и мало кто вообще помнит формулу Кардано). Знаю критерий неприводимости Эйзенштейна, он тут не подходит. Подскажите, как надо было доказать правильно?
Цитата:
Задача 11: Конечно ли множество различных подполей в

, изоморфных полю

?
Решение: Нет, континуально, потому что на изоморфные

подполя можно смотреть как на прямые на комплексной плоскости

, проходящие через ноль.
Цитата:
Задача 12: Найдите кубический многочлен с целыми коэффициентами, корнями которого являются квадраты корней многочлена

.
Не смог найти.
Цитата:
Задача 13: Существует ли матрица, характеристический многочлен которой равен

, а минимальный

, где
(1)

(2)

(3)

?
Если да, приведите пример такой матрицы. Если нет, докажите.
Решение:
(1) Следствие из теоремы Гамильтона-Кэли: минимальный многочлен матрицы делит характеристический. Поэтому здесь такой матрицы не существует.
(2) Во-первых, минимальный многочлен жордановой клетки

равен

. Во-вторых, степень

сомножителя

в минимальном многочлене есть наивысший порядок жордановых клеток, отвечающих собственному значению

.
В таком случае получаем матрицу

.
(3) Из сказанного выше понятно, что соответствующая матрица существует. Мне непонятен её вид. Сумма порядков жордановых клеток, соответствующих собственному значению

, равна

. Максимальный порядок такой клетки

. Как понять, есть две клетки порядка

и одна клетка порядка

или одна клетка порядка

и три клетки порядка

? Аналогично для другого собственного значения.
Цитата:
Задача 14: Найдите минимальный многочлен квадратной

матрицы

Знаю, что такой вид матрицы называется фробениусовой нормальной формой, для неё минимальный многочлен совпадает с характеристическим и равен

, но доказывать это не умею.



