Ломаю голову над противоречием, которое не могу уладить в голове.
Итак, как ясно из заглавия темы, я провожу некоторую серию испытаний Бернулли.
Для начала - описание процесса на пальцах. У меня есть некоторая точка. С некоторой вероятностью я позволяю ей стать плодотворной. Далее из этой точки с некоторой вероятностью я позволяю распуститься двум росткам (независимо). Тут уже возможны четыре варианта (думаю, ясно, какие). Из тех точек, к которым первой точке удалось выпустить ростки, я снова пытаюсь с некоторой вероятностью выпустить новые ростки. Так я продолжаю до тех пор, пока каждая из точек дерева не упустит все свои шансы.
Теперь более формально.
В принципе, последовательный рост дерева можно описать, как подбрасывание монеты несколько раз подряд. Вероятность успеха -

, как обычно. Соответственно, неуспеха -

или, для краткости,

. Теперь зададим регламент испытаний, чтобы последовательность успехов/неуспехов (с некоторыми оговорками) однозначно давала нам дерево.
Будем считать, что ростки из точки распускаются по диагонали вверх: один влево, другой в право. Распускаем их так, чтобы абсолютно все точки, испущенные (сквозь сколь угодно длинную цепочку поколений) из более левой точки, располагались левее абсолютно всех точек, испущенных более правой точкой. То есть, так, как, например, располагаются дерево Штерна-Броко:
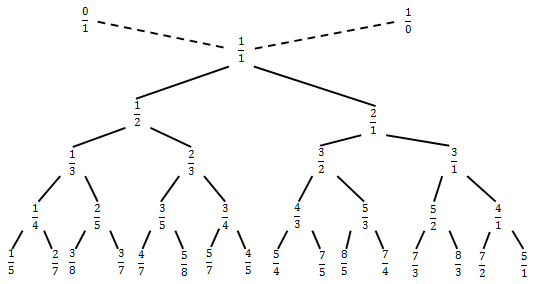
, -
только в нашем случае растут они вверх, а не вниз.
Теперь задаем регламент:
1. Берем самую левую точку уже имеющегося дерева, у которой не все шансы упущены. Если таких точек нет, завершаем последовательность.
2. Пробуем испустить левый росток подбрасыванием монеты;
если левый уже не может испуститься (в предыдущем испытании выпал неуспех), даем шанс правому.
3. Переходим к шагу 1.
Итак, у нас получится конечная последовательность

, которая однозначно определяет дерево.
По поводу разрешенных последовательностей. Назовем количеством шансов сумму по всем точкам количеств возможностей испустить росток (представим, как из точки вырастает мертвый пунктир, когда она терпит неудачу).
Дальше.
Количество шансов равно

Дерево выращено, когда

. Дерево имеет шанс вырасти еще, когда

Так как каждому выращенному дереву предшествует дерево, которое имеет шанс вырасти еще, то на окончательную последовательность

накладывается условие:

.
Соответственно, такая и только такая последовательность определит одно и только одно дерево. Обратно, любое дерево определяется какой-то последовательностью, и только ей.
Теперь к делу.
У нас определено пространство элементарных исходов, и сумма вероятностей всех различных деревьев должна быть равна единице. А именно:

,
где

- количество деревьев с n точками.
Первый вопрос: так ли это? Да, мне уже понятно, что единица странным образом выпадает, и это меня настораживает.
Второй вопрос. Если это так, то одна вещь не дает мне покоя:

,
но с другой стороны:

,
причем это должно работать для любого

.
Один из моих вариантов ответа на этот вопрос: следует учитывать и бесконечные деревья, и в случае

они имеют ненулевую вероятность в пространстве элементарных исходов.
Другой вопрос.
Я получил одно выражение для

(с учетом своей догадки о том, что сумма

равна единице только при

):

.
Для

оно дает

, однако мне удается построить только 12 деревьев. Где может быть ошибка? Или тут с самого начала все неверно?
Спасибо.
-- 06.07.2016, 13:13 --Так, со вторым вопросом я разобрался. Нашел недостающие деревья. Конкретно с этим пунктом помощь больше не нужна, спасибо.



