Мы занимаемся измерением поверхностей деталей с помощью измерительных систем.
Возникает такая задача. Дано: измеренные значения фактических точек поверхности детали и чертежные, идеальные значения точек поверхности чертежа детали.
На практике всегда имеются отклонения фактических точек вследствие неточного его изготовления. Нужно правильно оценить результаты измерений и определить степень годности или брака измеренных профилей детали относительно чертежных значений профилей. Есть допуск на отклонения фактических точек профиля поверхности 3D детали. Также есть допуск на смещения образа детали вдоль осей 0X, 0Y и поворота детали вокруг осей 0X, 0Z.
Допуск - это диапазон разрешенных отклонений измеренных фактических точек от чертежных.
Отсюда нужно правильно, как бы вписать, идеальную деталь в фактическую и оценить результаты отклонения фактических точек профиля поверхности 3D детали от идеальной 3D детали.
По величинам смещений и разворотов отклонений по контрольным точкам всех измеренных сечений детали далее ясно, как следует скорректировать технический процесс изготовления детали, чтобы последующие детали имели профиль полностью в допуске.
Возникает задача максимально возможного совмещения профилей детали с чертежом путем смещения образа детали вдоль осей 0X, 0Y и поворота детали вокруг осей 0X, 0Z (рис.1). Т.е. возникает задача минимизации числа точек за полем допуска или максимизации числа точек в поле допуска.
Проект, которым я сейчас занимаюсь, разрабатывался поколениями программистов до меня. В нем имеется готовая плавная функция

оценки числа фактических точек вне допуска в зависимости от смещения образа детали вдоль осей 0X (

), 0Y (

) и поворота детали вокруг осей 0X (

), 0Z (

).
Т.е. возникает задача поиска глобального минимума числа точек вне поля допуска в четырехмерном пространстве состояний перебором возможных значений четырех координат: смещения образа детали вдоль осей 0X, 0Y и поворота детали вокруг осей 0X, 0Z.
Отсюда у меня такой вопрос. Какой способ поиска глобального экстремума лучше применить?
Мне в голову пришло следующее. На первом этапе делаем некое подобие градиентного спуска: для начального положения в четырехмерном пространстве генерируем угловые точки, точки центров ребер, точки центра плоских квадратов, точки центра трехмерных кубов четырехмерного гиперкуба с центром в начальной точке поиска и сторонами, равными заданным шагам перебора координат

. На следующем шаге алгоритма точки с минимальным значением

становятся центрами новых гиперкубов.
Таким образом реализуется что-то вроде градиентного спуска - идет поиск положений с минимумом точек за полем допуска с заданными шагами

.
После того, как локальный минимум будет найден (найдено положение, которое больше нельзя улучшить при заданных шагах), то реализуется второй этап:
Положение с минимальным значением точек за полем допуска становится центром гиперкуба

.
Внутри этого гиперкуба методом дихотомии (бисекции) реализуется поиск положения с минимальным значением числа точек за полем допуска. Критерий остановки - заданный минимальный шаг дихотомии
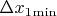
,

,

,

.
Недостаток описанного метода - реализуется поиск только локального минимума. Глобальный минимум мы можем пропустить. Что можно сделать, чтобы гарантированно получить глобальный минимум?



