daogiauvangКрасивая задачка! Первая половина что-то мне напоминает про бабочку..
А вот картинки я рисовать не умею....
1.Опустим из центра

перпендикуляр

на хорду
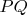
: он попадает в ее середину:

. Углы

и

- прямые, так что точки

лежат на одной окружности. Поэтому углы

и

равны (как вписанные). Рассмотрим треугольники

(с медианой

) и

(с медианой

): они подобны (сначала получим подобие их половинок

и

- по двум углам; отсюда получим пропорциональность их сторон; это даст пропорциональность пары сторон других половинок

и

, но там есть и равные углы . Значит, есть подобие ).
Получили: угол

равен углу

. Но последний равен углу

. Это дает параллельность

и

. Аналогично получим параллельность

и

, и параллелограмность

, откуда и следует равенство отрезков...
Нда...
2. Получили задачу: в параллелограмме

из вершины

опустили перпендикуляры

и

на продолжения сторон пар-мма.

- точка пересечения отрезков

и

. доказать:

ортогонально
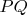
.
a)(Вектора) Пусть

. Тогда

. Имеем: вектор

есть взвешенная сумма векторов

и

, с некими весами

и

, а также векторов

и

(с какими то весами

и

). Из этого векторного равенства получим простенькую систему на

. Решив ее, выразим вектор

через

и

, и неожиданно обнаруживаем, что он коллинеарен вектору

!!!
б) Заметим, что вектор

получается из вектора

поворотом на

и растяжением в

раз (

- угол при вершине

). Соответственно, вектор

также получается из вектора

такими же поворотом и растяжением. Значит, вектор

получается из вектора

(а он, напомню, коллинеарен

) поворотом и растяжением. Это дает нужную ортогональность...



