Магнитная индукция и напряженность в постоянном магните.

[Saber]

Доброго времени суток, форумчане. Работал с постоянным магнитом (цилиндрическим магнитом) в программе максвелл и при выводе графиков получил отличающиеся друг от друга картины поля. В случае индукции график имеет форму перевернутой параболы, а в случае напряженности, на вершине этой параболы образовывается впадина, из-за чего график имеет два максимума. Чтобы разобраться в причине получил две картины векторного распределения поля. Для индукции линии поля направлены из северного поля в южный, причем внутри и снаружи векторы сонаправленные. Когда же я построил вектора напряженности, оказалось, что внутри и снаружи направления отличаются. Это и является причиной "впадины" на вершине графика напряженности. Внимание вопрос: в чем причина такого поведения поля? Почему в случае индукции они направлены в одном направлении, а в случае напряженности в разные? Как это объясняется с физической точки зрения? Намагниченность направлена от одного круглого основания к другому.
Заранее благодарю за помощь!

[AnatolyBa]

График чего? Зависимость индукции/напряженности от чего?
Впрочем, не столь важно. Для напряженности важно помнить, что циркуляция по замкнутому контуру равна сумме внешних токов которые контур охватывает.
Внешних, а не внутренних молекулярных, т. е. для постоянного магнита циркуляция равна нулю. Поэтому напряженность вмутри и снаружи направлена противоположно и на торцах испытывает скачек.
Индукция же, точнее ее нормальмая к поверхности раздела сред составляющая, обязана быть непрерывна. Поэтому индукция внутри и снаружи направлена одинаково.
Намагниченность же, нулевая снаружи и ненулевая внутри, как раз и обеспечивает скачек напряженности при непрерывной индукции.

[Saber]

AnatolyBa в сообщении #1126986 писал(а):

График чего? Зависимость индукции/напряженности от чего?
Впрочем, не столь важно. Для напряженности важно помнить, что циркуляция по замкнутому контуру равна сумме внешних токов которые контур охватывает.
Внешних, а не внутренних молекулярных, т. е. для постоянного магнита циркуляция равна нулю. Поэтому напряженность вмутри и снаружи направлена противоположно и на торцах испытывает скачек.
Индукция же, точнее ее нормальмая к поверхности раздела сред составляющая, обязана быть непрерывна. Поэтому индукция внутри и снаружи направлена одинаково.
Намагниченность же, нулевая снаружи и ненулевая внутри, как раз и обеспечивает скачек напряженности при непрерывной индукции.

Ой, да, прошу прощения, магнитная индукция и напряженность от расстояния.

[rustot]

Вне магнита $\vec{B}$ и $\vec{H}$ одинаковы (в сгс просто равны, в си с каким то коэффициентом пропорциональности), если вы получили вне магнита разные величины то это какая то ошибка. может у вас в программе не вакуум вне магнита а среда с какой то намагниченностью.

В теле же магнита из $\vec{H}$ (по сравнению с $\vec{B}$) вычитается намагниченность $4\pi \vec{M}$, так что как правило она меняет направление на противоположное.

То есть для цилиндрического магнита, однородно намагниченного вдоль оси, $\vec{H}$ выглядит везде в точности как электрическое поле плоского конденсатора с круглыми обкладками вдоль граней цилиндра, а $\vec{B}$ совпадая с $\vec{H}$ вне, внутри "конденсатора" ни направления не меняет ни скачка модуля не имеет

Откуда вообще "возникает" $\vec{H}$? Возьмем уравнение

$\nabla\times\vec{B} = \frac{4\pi}{c}\vec{j} + \frac{1}{c}\frac{\partial}{\partial t}\vec{E}$

Оно верно в том числе и для поля в среде, но только если вы в $\vec{j}$ впишете поштучно все заряды этой самой среды. Но записать его можно по разному. Например можно выразить ток через производную от интегральной величины "сколько и куда всего протекло через точку заряда начиная с какого то момента времени" $\vec{P} = \int_{t_0}^t \vec{j}(t) dt$ и соответственно $\vec{j} = \frac{\partial}{\partial t}\vec{P}$. 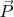Причем так можно описать хоть весь имеющийся ток (например постоянный ток в кольцевом проводнике можно описать как непрерывно растущую $\vec{P}$) так и какую то его подчасть. 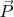Если из всех имеющихся зарядов выделить те, которые в среднем не меняют своего положения а лишь в каких то пределах от него отклоняются, то выразить именно эту погруппу зарядов через $\vec{P}$ как раз очень удобно, потому-что вопрос "с какого то момента времени" решается очевидным образом - с момент когда они все занимали это среднее положение. Тогда получаем

$\nabla\times\vec{B} = \frac{4\pi}{c}(\vec{j} + \frac{\partial}{\partial t} \vec{P}) + \frac{1}{c}\frac{\partial}{\partial t} E$

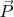
Где в $\vec{j}$ входят уже не все заряды, о только оставшиеся за вычетом тех самых "слегка смещающихся". Тут напрашивается объединение поля и этой величины $\vec{P}$ в целях удобства в композитную величину $\vec{D} = \vec{E} + 4\pi\vec{P}$, чтобы получить короткую запись

$\nabla\times\vec{B} = \frac{4\pi}{c}\vec{j} + \frac{1}{c}\frac{\partial}{\partial t} \vec{D}$

На этом возможности альтернативно записать $\vec{j}$ не исчерпываются. Например если $\vec{j}$ или какое то его слагаемое непрерывно, сохраняет плотность заряда везде неизменной, то есть $\nabla\vec{j} = 0$, то его можно записать в виде ротора другого поля $\vec{j} = c\nabla\times\vec{M}$. Как и в предыдущем случае, хотя формально и макроскопический постоянный ток в кольцевом проводнике тоже можно описать через $\vec{M}$, используется эта форма представления тока там где удобно, в микротоках в среде (впрочем если кольцевой проводник в задаче рассматривается как материальная точка - источник поля, то и для него используется). Допустим движение заряда по орбите, размеры которой много меньше чем детализация с которой мы рассматриваем поле, удобно характеризовать именно через $\vec{M}$ вместо $\vec{j}$. Таким образом "выкусив" из полного тока $\vec{j}$ очередную порцию зарядов в другом представлении мы получаем

$\nabla\times\vec{B} = \frac{4\pi}{c}\vec{j} + 4\pi\nabla\times\vec{M} + \frac{1}{c}\frac{\partial}{\partial t} \vec{D}$

И как и в предыдущем случае напрашивается объединение $\vec{H} = \vec{B} - 4\pi\vec{M}$

$\nabla\times\vec{H} = \frac{4\pi}{c}\vec{j} + \frac{1}{c}\frac{\partial}{\partial t} \vec{D}$

Таким образом $\vec{D}$ и $\vec{H}$ получаются путем объединения полей $\vec{E}$ и $\vec{B}$ с некоторым унифицированным поведением части имеющихся зарядов, которые вместе определены как "среда", на фоне которой в уравнениях в качестве $\rho$ и $\vec{j}$ рассматриваются только оставшиеся заряды, в "среду" не включенные