У вас что, так много подобных условий? Как по мне, вполне себе метод. Более того (это уже касательно вашего преобразования для равенств), решать две задачи попроще вполне может оказаться быстрее и точнее, чем одну задачу посложнее.
да, немало (там из геометрической задачи вытекает, например, условия на касание двух прямоугольников - могут касаться или сверху, или снизу, или слева, или справа, см.
dxdy.ru/topic108768). к тому же они начинают "перемешиваться" с конъюнкцией, и выдирать отдельно эти все варианты - очень сильно уменьшает читабельность и как следствие увеличивает ошибки.
намекаете на то, что дизъюнкцию можно записать как

? хм.. может быть, и подойдет (ведь, я ничего не путаю,
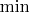
может быть представлен через арифметические операции и взятие модуля?)
Думал так (с нулем не работает):

.
нет, для случая

и

тоже не сработает.