Задача прямоугольного разбиения с ограничениями

[_hum_]

Столкнулся с задачей разбиения прямоугольной области на прямоугольники с ограничениями (архитектурная планировка квартиры). Нормальной литературы по данной проблематике почему-то не нашел (большинство запросов по ключевым словам rectangular partition дает ссылки на задачи наподобие задачи укладки двумерного ранца), потому немного в растерянности.
Из того, что более-менее можно было бы перенести на мою проблему - подход к задаче максимального прямоугольного покрытия области, сформулированная с точки зрения нелинейного программирования. А именно, ищется минимум функции (принимающей нулевое значение только при непересекающихся комбинациях прямоугольников)

$$\sum_{i=1}^{m-1}\sum_{j = i + 1}^{m}\max\big\{0,\frac{(w^i + w^j)^2}{4} - (C_x^i - C_x^j)^2\big\}^2\max\big\{0,\frac{(h^i + h^j)^2}{4} - (C_y^i - C_y^j)^2\big\}^2,$$

(где $C^i = (C_x^i, C_y^i)$ - центр прямоугольника, $w^i , h^i$ - его ширина и высота соответственно) при ограничениях невыхода прямоугольников за пределы области.
Но вопрос, насколько такой подход для моего случая будет вычислительно затратный по сравнению с использованием комбинаторных эвристических алгоритмов? (У меня пока нет интуиции в этом - кажется и там, и там производится перебор вариантов, и не совсем понятна выгода).

Спасибо.

п.с. А зачем максимумы в этом подходе возводят в квадраты? Все равно же функция остается не всюду дифференцируемой...
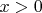
п.п.с. И как в задачах математического программирования обрабатываются ограничения с условиями наподобие "или"($x > 0$ или $x < -1$)?