Количество траекторий

[Roman Kotyk]

Пусть $k \ge 2, m, n - $ заданные натуральные числа, причем $k>|m-n|$. Кузнечик хочет с начала координат точки $(0;0)$ добраться точки $(m;n)$, двигаясь прыжками, каждый из которых либо на $1$ вверх или же на $1$ вправо. Найти количество траекторий кузнечика, которые не имеют общих точек с прямыми $y=x+k$ и $y=x-k.$

[DeBill]

В книжке Виленкина по вероятности решается классическая задача про рубли и полтинники....
Почему бы не использовать ту же методу?
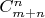
Всего путей из начала в конец $C^n_{m+n}$. Но есть плохие пути - те, которые пересекают. Давайте путь, пересекший (впервые) запрещенную линию, отразим симметрично относительно ее. Концевая точка перейдет при этом либо в точку $(m-k,k+n)$, либо в точку $(n-k,k+m)$. Посчитав кол-во путей, идущих в эти точки, и вычитая их, получим ответ
$C^n_{n+m} - C^{m-k}_{m+n} - C^{n-k}_{n+m}$ (цешки с отрицательными индексами - зануляем, как обычно)...