Так что нужно? Доказать, что существует хотя бы один корень или что хотя бы один из корней имеет ненулевую мнимую часть?
-- 22 апр 2016, 13:45 --Наличие корней у алгебраического уравнения это "Основная теорема алгебры", и если нужно узнать, если ли (возможно, но не обязательно, комплексный) корень - есть. Для любых коэффициентов. А если нужно узнать, есть ли "существенно комплексный" корень, в смысле не являющийся действительным числом - я бы воспользовался "Правилом Декарта"
Цитата:
Теорема Декарта или правило знаков Декарта, — теорема, утверждающая, что число положительных корней многочлена с вещественными коэффициентами равно числу перемен знаков в ряду его коэффициентов или на чётное число меньше этого числа (корни считаются с учётом кратности, нулевые коэффициенты при подсчёте числа перемен знаков не учитываются).
То есть считаем число положительных корней (или его оценку сверху, отличающуюся на чётное число), подставляем вместо x

, считаем число отрицательных (и нулевые ещё проверим) и если получится в сумме меньше степени многочлена - точно есть такие, которые не положительны, не отрицательны и не ноль. Очевидно, что если у исходного многочлена максимальное число перемен знака (4), то у
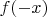
их вовсе нет. Вот аккуратно проверить возможность того, что у

3 перемены и у
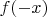
тоже три - мне лень, прошу прощения. Хотя несложно - выписать 16 вариантов знаков и посчитать. Кажется, что не будет.



