Всем доброго времени суток. Помогите плз с задачами:
1. Определить индукцию магнитного поля в точке

, если проводник с током имеет вид, показанный на рисунке. Сила тока в проводнике, радиус, магнитная проницаемость:

известны.

Правильно ли я понимаю, что:

?, где:

- индукция в центре витка с током
2. Вдоль бесконечной прямолинейной тонкостенной трубы течет ток. Определить индукцию

магнитного поля в произвольной точке внутри трубы, если сила тока равна
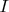
.
По логике, в центре трубы вектора

от токов на противоположных стенках направлены встречно и

. А как определить

в любой точке внутри трубы?