System of equations (two variables - two equations)

[ins-]

Solve in real numbers the system:
$x^2+3xy+y^2-8x-7y+6=0$
$2x^2+4xy+3y^2-12x-16y+13=0$

(I created this system and know how to solve it, but I'm interested to see the level of difficulty and different approaches.)
It can be rewritten as $(x-1)^2+3(x-1)(y-2)+(y-2)^2=\operatorname{const}_1$ and $2(x-1)^2+4(x-1)(y-2)+3(y-2)^2=\operatorname{const}_2$.

[Karan]

This problem is too easy to be in the olympiad forum. Please provide your solution, after that you can discuss different approaches in the main forum.

[Karan]

Тема перемещена из форума «Олимпиадные задачи (М)» в форум «Карантин»
по следующим причинам:

- отсутствуют собственные содержательные попытки решения задач(и).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Karan]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (М)»

[DeBill]

Эллипс и гипербола. Приводит к уравнению 4-й степени, вообще говоря.
Но - пробуем: находим центр каждой. О, чудеса : центры совпали (как это и продемонстрировал ТС).
Ну, тогда - легко: избавляясь от $\operatorname{const}$, получим однородное уравнение, из него найдем $\frac{x-1}{y-2}$, и т.д....

[ins-]

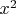
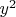
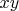
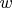
I downloaded interesting book for a systems and thought about finding a common method for solving similar systems in a pure algebraic way (without using conics). I found something that works for all the similar systems in the book. Take the coefficients before $x^2$, $y^2$, $xy$. Let them be $u$, $v$, $w$ - they are fixed numbers. Then try to find a representation of the form $u(x-a)^2+v(x-a)(x-b)+w(x-b)^2$. 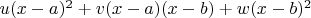After expanding the brackets a system of first degree can be formed for $a$ and $b$ using the coefficients before $x$ and $y$. I'm wondering for what kind of similar systems it works. Probably not for all possible. I suppose it works when a "linear combination" of the initial equations can be factorized or the centers of the two conics are the same.