Произведение непрерывных функций

[RabbitXO]

Пусть $f:X_1\rightarrow\mathbb{C}$, $g:X_2\rightarrow\mathbb{C}$ непрерывные функции на топологических пространствах $(X_1,\tau_1)$, $(X_2,\tau_2)$ соответсвенно. Будет ли функция $f\cdot g:X_1\times X_2\rightarrow \mathbb{C}$, $(x_1,x_2)\mapsto f(x_1)g(x_2)$ непрерывной на $X_1\times X_2$?

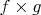
Пусть $f\times g$ прямое произведение функций, т.е. $f\times g:X_1\times X_2\rightarrow\mathbb{C}^2$, $(x_1,x_2)\mapsto (f(x_1),g(x_2))$.
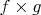
Таким образом произведение $f$ и $g$ можно представить, как $f\cdot g= \cdot \circ(f\times g)$. Требуется показать, что $f\times g$ непрерывна на $X_1\times X_2$.

Пусть $U,V$ открытые подмножества $\mathbb{C}$. Тогда $U\times V$ элемент базы $\mathbb{C}^2$.

$$ (f\times g)^{-1}(U\times V)= f^{-1}(U)\times g^{-1}(V)\in \tau_1\times\tau_2, $$

где $\tau_1\times\tau_2$ база $X_1\times X_2$.

Где я ошибся?

Спасибо.

[oskar_808]

Нигде не ошиблись, всё верно. Вообще, для любых топологических пространств $X$, $Y$, $Z$, $W$ и любых двух непрерывных функций $f\colon X\to Z$ и $g\colon Y\to W$ отображение $f\times g\colon X\times Y\to Z\times W$ непрерывно. Это следует из того, что операция $\times$ определяет произведение в категории топологических пространств.

[DeBill]

RabbitXO
Да в общем, нормально. Только одна деталь:

RabbitXO в сообщении #1106258 писал(а):

Пусть $U,V$ открытые подмножества $\mathbb{C}$. Тогда $U\times V$ элемент базы $\mathbb{C}^2$.

А, по логике вещей, рассуждение должно проходить чуть иначе: Пусть $W$ - элемент некоторой базы топологии в..., и т.д.. Дырочка залатается, если Ваши рассуждения дополнить фразой: всевозможные пары $U\times V$ образуют базу.

[RabbitXO]

Не совсем аккуратно вышло.

Всем спасибо.