Топология нормированного пространства

[Anton_Peplov]

Пусть $L$ - нормированное линейное пространство. Возьмем каноническую метрику, порожденную этой нормой, и рассмотрим топологию, индуцированную этой метрикой.

Назовем преобразованием подобия функцию $L \to L$ вида $y = \alpha x + b$, где $\alpha\ne 0$.
(Как-то такая функция в учебнике линейной алгебры называлась, но я забыл. В школе для $\mathbb{R} \to \mathbb{R}$ ее называли линейной функцией, но здесь такое название будет злом, ибо легко спутать с линейным оператором. Насколько я понимаю, это то самое преобразование подобия, о котором детям рассказывают в школьной геометрии. Взять фигуру, перенести в другое место и/или растянуть/сжать).

Назовем два множества $A$ и $B$ подобными, если есть такое преобразование подобия $f$, что $f(A) = B$. Очевидно, что это отношение эквивалентности. Назовем класс всех множеств, подобных множеству $A$, классом подобия $A$.

Лемма 1. Множество, подобное открытому, открыто.

Лемма 2. Если $A$ ограничено, то в любом открытом шаре найдется $B$, подобное $A$.

Основное утверждение. Класс подобия любого открытого ограниченного непустого множества $A$ образует базу топологии $L$.

Рассмотрим такой класс $\Omega$ множеств, подобных $A$. По лемме 1, его элементы открыты. Чтобы доказать основное утверждение, нам надо доказать, что:
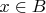
1. Для любого $x \in L$ найдется $B \in \Omega$ такое, что $x \in B$. Это легко: берем $A$ и параллельным переносом пуляем его в точку $x$.
2. Если $B_1, B_2 \in \Omega$ и $x \in B_1 \cap B_2$, то найдется $B_3 \in \Omega$ такое, что $B_3 \subset B_1 \cap B_2$ и $x \in B_3$.
Тут и пригодится лемма 2. $B_1 \cap B_2$ открыто, значит, включает открытый шар с центром в точке $x$. По лемме, в этом шаре найдется $C$, подобное $A$. Уменьшим $C$ до половины радиуса шара и сдвинем параллельным переносом в точку $x$. Вуаля - получили элемент класса подобия, содержащий точку $x$ и содержащийся в $B_1 \cap B_2$.
Теорема доказана набросок доказательства закончен.

Вопрос простой: у меня все правильно или я где-то напахал?

P.S. Все это витийство родилось из осмысления того факта, что базу на канонической плоскости образуют не только открытые круги, но и открытые квадраты. И мне очень захотелось доказать, что базу образуют также открытые жирафики.

[demolishka]

Anton_Peplov в сообщении #1106092 писал(а):

Уменьшим $C$ до половины радиуса шара

Не совсем понятно, но надо бы так: найдем $C',$ подобное $C$, в шарике радиуса $\frac{\varepsilon}{2}$ с центром в точке $x.$ И потом уже $C'$ сдвигаем.
А вообще надо изначально было брать такое $C$.

[Xaositect]

Это называется гомотетия.

Доказательство верно.

[Mikhail_K]

Anton_Peplov в сообщении #1106092 писал(а):

Рассмотрим такой класс $\Omega$ множеств, подобных $A$. По лемме 1, его элементы открыты. Чтобы доказать основное утверждение, нам надо доказать, что:
1. Для любого $x \in L$ найдется $B \in \Omega$ такое, что $x \in B$. Это легко: берем $A$ и параллельным переносом пуляем его в точку $x$.
2. Если $B_1, B_2 \in \Omega$ и $x \in B_1 \cap B_2$, то найдется $B_3 \in \Omega$ такое, что $B_3 \subset B_1 \cap B_2$ и $x \in B_3$.

Так Вы доказали только то, что "класс подобия" является базой некоторой топологии, но не доказали, что той же самой, исходной топологии в $L$. Там ещё условие 3-е надо доказывать, посмотрите.
Но в целом, похоже на правду.

[Anton_Peplov]

Xaositect
Спасибо!

-- 12.03.2016, 22:21 --

Mikhail_K в сообщении #1106104 писал(а):

Так Вы доказали только то, что "класс подобия" является базой некоторой топологии, но не доказали, что той же самой, исходной топологии в $L$.

Да, это у меня пробел. Но условие 3 тоже легко доказывается из леммы 2.

[Mikhail_K]

Anton_Peplov в сообщении #1106105 писал(а):

Да, это у меня пробел. Но условие 3 тоже легко доказывается из леммы 2.

Да, согласен.