Вот кусочек бипризмы Френеля, на которую падает луч под углом

. Хочу найти угол

. Зашел в тупик, а ни в одной книге не написано, как найти этот угол.
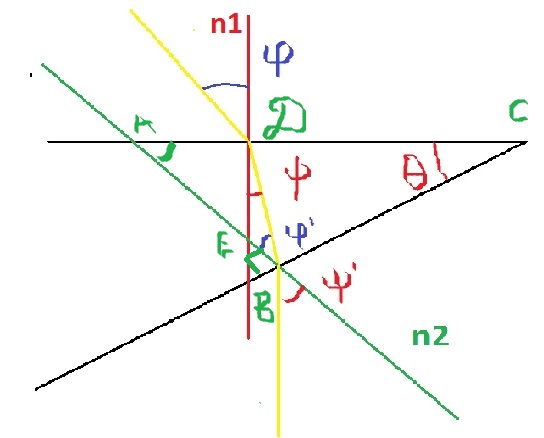
Рассмотрим треугольник

. Он, очевидно, прямоугольный,

Я пришел к выводу, что угол

будет углом преломления, если нормаль

будет параллельна падающему лучу. Это значит, что угол

При этом

, тогда

Т.е.

Т.к.

- преломляющий угол призмы, очень мал, то и

будет очень малым.
Из рисунка видно, что

И получается три условия, два из них - это законы Снелла:



Из этих трех условий можно составить уравнение, которое будет содержать только показатель преломления, угол

и угол

. Но оно имеет сомнительный вид.
-- 08.03.2016, 12:49 --Все говорят, что угол

, но никто не хочет этого доказывать.



