Шары и ящики

[Omega]

DeBill, то есть всё-таки Вы думаете правильно?

[DeBill]

Omega в сообщении #1102009 писал(а):

не суть важно какова природа этого "случайного" процесса.

Ну как же не важна, когда - архиважна!
Посмотрите на те 2 модели, что я описал выше. Проверьте, что - для упрощенной задачи TOTAL в одной моделе
ответ $\frac{2}{9}$, а в другой - как у вас, 0.4

[Omega]

DeBill, ну хорошо, раз так, то вот - мне тут подсказали, что эта задача похоже на задачу заполнения купейного вагона людьми. И действительно :).

[DeBill]

Omega в сообщении #1102016 писал(а):

DeBill, то есть всё-таки Вы думаете правильно?

В смысле - я думаю правильно? Спасибо!
Или в смысле: я думаю, что у вас - правильно?
Это вопрос о выборе модели? Или о Вашем счете?
О модели: мне кажется, да, постановке задачи более отвечает случайный выбор именно места для шарика, а не ящика.
Но лишь "кажется", т.к. из описания эксперимента неясно, кто правее: мы с вами, или TOTAL

[Omega]

Я говорю про вариант решения, который я предложил пару сообщений назад.

[DeBill]

Omega в сообщении #1102018 писал(а):

эта задача похоже на задачу заполнения купейного вагона людьми

Ох! Сначала было обрадовался: вот, все понятно, наша модель! Но: кто заполняет вагон народом? Комп, который распределяет народ на свободные МЕСТА? Или это чел наугад тыкается в купе, смотрит: если места есть, выбирает его - место -наугад; если нет - идет дальше, снова наугад тыкается в КУПЕ, и т.д......

-- 25.02.2016, 16:51 --

Omega в сообщении #1102022 писал(а):

Я говорю про вариант решения,

Дык я ж написал: подход - хорош, счет - совсем нет

[provincialka]

Omega в сообщении #1102009 писал(а):

Будем считать равновероятным выбор корзины и попадания одного шара в любую из них.

В том числе в "полную"? Или вы выбираете только те корзины, которые не заполнены?

Omega в сообщении #1102009 писал(а):

По-моему задача вполне понятная.

Завидую вам. Мне так она не понятна.

[DeBill]

Omega

Или сравните Ваше $N_1$ для 4-4-4-1-1 с правильным $\frac{5!}{3! \cdot 2!} \cdot (C^4_4)^3 \cdot (C^1_4)^2$

[Omega]

provincialka, нет нет, тут такое дело, - если ящик заполняется попасть в него нельзя. И соответственно вероятность попасть в него становиться нулевой.
DeBill, не пойму как Вы так считаете. Я - вот по какому принципу:

$$N_{1}=5! \cdot \left (C_{5}^{1} \cdot C_{14}^{4}+C_{4}^{1} \cdot C_{10}^{4} + C_{3}^{1} \cdot C_{6}^{4}+C_{2}^{1} \cdot C_{2}^{1}+C_{1}^{1} \cdot C_{1}^{1} \right)$$

Всего пять факториал вариантов расставить пять ящиков как угодно. Затем выбираем из пяти один определённый ящик и заполняем его (выбираем 4 шара из 14), далее - из 4 ящиков выбираем снова один определённый, в него снова из оставшихся 10 шаров - выбираем 4 и т.д.

[DeBill]

Omega
Нет, Ваш счет совершенно неправильный.
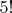
1. Зачем нам $5!$, коль мы затем все равно будем выбирать один из пяти?
2. Шары мы полагаем неразличимыми - это видно из того могучего знаменателя, на который потом будем делить.
Так что не надо выбирать 4 из 14.
3. Далее - один из 4-х, и в нем снова будет 4 шара. Двойной счет:вы одну и ту же пару (сначала - тот ящик, а потом - этот, но могло быть: сначала - этот, а потом - тот) посчитали дважды...
4. Почему вы складываете варианты, когда их надо перемножать? И т.д.
Короче, все неправильно.
Посмотрите на мою формулу, и попытайтесь понять логику ее сочинения.
ЗЫ Я посчитал по вашему способу (но правильно), и по другому - я писал выше, с вычитанием. Как и ожидалось, второй - короче. Ну да бог с ним - сделайте - до конца - вашим методом. Проблема в том, что ответы для этих двух способов - не сошлись....И лишь после двойной проверки я наконец заметил, что Вы пропустили вариант 44222...(теперь - сходится).

-- 25.02.2016, 17:49 --

38160

[Omega]

DeBill, и действительно я подумал: то как я считаю - не верно. Спасибо.
Но формулу для $N_{i}$ я так и не осознал, почему Вы так считаете. Объясните пожалуйста.

[Lia]

Omega
Напоминаю Вам, что правила форума запрещают давать полные решения учебных задач. Вам осталось фактически понять все, сказанное выше.

Тем более, что оно настолько плотно граничит с полным решением (и содержит все возможные подсказки), что плотнее некуда.

[Omega]

Lia, ну что Вы сразу-то начинаете...

Вот, смотрите - например для комбинации "4-4-2-2-2":

$$N = \overbrace{\left(\frac{5!}{2! \cdot 3!}\right)}^\substack{\text{перестановки}\\ \text{с повторениями}}} \cdot \overbrace{ \left(C_{4}^{4} \right)^{2}}^\substack{{\text{рассаживаем четверых} \\ \text{по четырём местам}}}} \cdot \overbrace{ \left(C_{4}^{2} \right)^{3}}^\substack{{\text{рассаживаем двоих} \\ \text{по четырём местам}}}}$$

Верно?

[Lia]

(Оффтоп)

Omega в сообщении #1102044 писал(а):

Lia, ну что Вы сразу-то начинаете...

Еще и не планировала. Но могу.

Верно. Вот и продолжайте.

[DeBill]

Omega
Ну да. Только что это за перестановки? Откуда они взялись? Почему для другого набора - на предыд. странице - все не так? Почему одно - в квадрате, а другое - в кубе?
ЗЫ Я б еще чё сказал - да боюсь сильно модератора - замордерирует он(а) меня.... .