Добрый день, уважаемые участники!
Помогите, пожалуйста, разобраться с задачей по общей топологии. Эта задача взята из учебника В. А. Васильева "Топология для младшекурсников", стр. 13. К своему стыду, я над ней бьюсь уже 3-ий день и никак не могу поверить, что такие задачи решают, как написано в аннотации, "старшеклассники и младшекурсники". Итак, текст задачи (привожу без изменения).
Пусть

— множество линейных отображений

в себя, а топология в нем задается его очевидным отождествлением с

. Отношение эквивалентности:

, где

— какая-нибудь обратимая матрица. Требуется описать фактормножество

и фактортопологию. Выясните, в частности, является ли пространство

хаусдорфовым.
Где я застрял: не могу определить фактортопологию. Но по порядку.
Что мне уже известно. Поскольку по условию

— это обратимая, а, следовательно, невырожденная матрица, то её можно рассматривать как матрицу перехода от одного базиса в

к другому. Так как рассматриваются все такие матрицы, то я предполагаю, что в классе эквивалентности будут матрицы одного и того же оператора во всевозможных базисах. Таким образом, каждому классу эквивалентности сопоставляется некий оператор.
Далее, поскольку спектр не меняется при переходе к новому базису, то оператор однозначно определяется своими собственными значениями. Однако они не упорядочены, то есть,

есть то же самое, что и

.
В итоге получаем полуплоскость, ограниченную прямой

. Я при решении обозначил ось абсцисс

, ось ординат —

. Тогда получаем, например, такую полуплоскость:

.
Однако это не все возможные спектры, ибо ещё могут быть комплексносопряжённые значения:

. Здесь нам также достаточно лишь полуплоскости

, что для удобства можно представить следующим образом: к нашей системе координат

добавим ось аппликат

, и тогда полуплоскость

"приклеим" к полуплоскости

вдоль прямой

.
В результате этих рассуждений приходим к тому, что фактормножество суть

. Почему "суть" — потому что пока не гомеоморфно, ведь структура открытых множеств не ясна.
Вот тут-то я и встрял. Я попробовал проверить тривиальный случай: не является ли фактортопология дискретной? Ну, вдруг так задачка подобрана. Очевидно, не является. Контрпример:

Для произвольной матрицы

спектр определяется так:

. Тогда для фиксированных с. зн.

имеем:

В операторе из контрпримера у матриц либо

, либо

, тогда эта часть полного прообраза представляет собой "кресты", расположенные в двух точках в

:

и

. Если же ни

, ни

не равны нулю, то эта часть полного прообраза будет представлять собой довольно интересные поверхности, уходящие на бесконечность:

В общем, такое множество (полный прообраз спектра

) точно не является открытым, так как никакой шар с центром в точке

не будет полностью содержаться в нём, ибо точка

не принадлежит ему.
Да, кстати, поскольку в условии не сказано, какая топология задана на

, то я по умолчанию считал, что стандартная, метрического пространства (с шарами которая). Тем более, что в книжке раньше делались намёки, что, если не сказано иначе, имеется в виду стандартная. "Очевидное отождествление", насколько я понимаю, это следующее:

.
Согласно определению, открытыми в фактортопологии считаются те множества, полные прообразы которых при канонической проекции

будут открытыми. Я пробовал найти полные прообразы для открытых кругов в

, это ну ооочень нетривиально. И потом, там получается два уравнения для четырёх неизвестных (случай
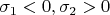
):

что явно намекает на поверхность в четырёхмерном пространстве, а уж коль скоро это поверхность, то никак не открытое множество в стандартной топологии.
Чётко поставленных вопроса у меня три.
1. Не ошибся ли где-то в своих выкладках и рассуждениях, в том числе, в интерпретации задачи?
2. Как поступать дальше, возможно, есть какие стандартные приёмы для таких задач? Как искать открытые множества в фактортопологиях — что, как всегда, угадывать?

3. Неужели такое реально решают старшеклассники в 57-ой школе?

Спасибо всем, кто возьмётся помочь, любым замечаниям и подсказкам буду рад.
С хаусдорфовостью, полагаю, я сам разберусь, если узнаю топологию.