Итак, ход решения при

.
Запишем доказываемое неравенство в виде

Вычтем одно и то же из обеих частей и будем доказывать, что

Проще всего с правой частью. Берём интегралы явно, разлагаем арксинус и ещё кое-что в ряд Тейлора, получаем, что асимптотически правая часть представляет собой

. Кроме того, если использовать вместо ряда Тейлора формулу Тейлора с достаточным количеством членов и остаточным членом, удаётся доказать, что правая часть больше или равна

при любом

. Остаётся доказать, что левая часть, наоборот, меньше или равна этого выражения.
В левой части тоже берём интегралы. То, что
под знаком суммы, получается равным

Тут весьма к месту оказывается формула

В результате выражение под суммой записывается в виде
![$$
\frac{2}{ab}({\rm{arcsin}}\Delta-\Delta),\quad \Delta=b\sqrt{1-a^2}-a\sqrt{1-b^2}\in [0,1].
$$ $$
\frac{2}{ab}({\rm{arcsin}}\Delta-\Delta),\quad \Delta=b\sqrt{1-a^2}-a\sqrt{1-b^2}\in [0,1].
$$](https://dxdy-02.korotkov.co.uk/f/d/f/1/df1533e8453dc19d541b82d29a2cff3d82.png)
Снова разлагаем арксинус в ряд. Асимптотически

есть

, причём

стремится к нулю равномерно по
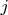
при

. Можно написать, что

Подставляем эту оценку, и в левой части доказываемого неравенства получается сумма

Для

можно получить оценку:



И у нас получается сумма

Под суммами убывающие функции, поэтому сумма

1-е слагаемое

соответствующий интеграл. Оцениваем, считаем, получается, что левая часть неравенства асимптотически есть

, где

. Ура.
А если не асимптотически? Тогда надо оценивать

. Это можно сделать, опять же, применяя формулу Тейлора с остаточным членом - там, где этот

впервые появляется. Получается гораздо хуже, чем с правой частью. У меня после ряда оценок получилось, что левая часть (при любом

) меньше или равна

Эта вещь меньше, чем

при

. Тем самым, при

неравенство доказано.
Не беда, что оно не доказано при

: в конце концов, конечное число неравенств можно просто проверить на компьютере.
Признаюсь, что задача - не из сборника олимпиадных задач: это реальная проблема, с которой я встретился в процессе исследований. Так что наличие "красивого" решения не гарантировано.
Моё решение очень громоздко, но неоднократные проверки показали, что ошибок нет.
Мне бы вот ещё доказать это неравенство при

... Может быть, возможно это сделать с опорой на то, что оно верно при

...