С другой - события
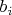
(ясно что не "

") могут рассматриваться как элементарные со своими вероятностями - и никакого криминала.
Если это элементарные исходы, то в таком случае ФПВ тем более ни при чём: и событие

, и событие

, и событие

- все состоят из элементарных исходов, и

- это просто сумма вероятностей элементарных исходов, принадлежащих

.
А напишите для дальнейшего совершенствования полный ответ без формулы полной вероятности и чтобы не "на худой конец", а в идеале.
Вы его и так уже почти написали:

А универсального способа вычисления вероятностей типа

и

в общем случае пока не изобретено: всякий раз приходится использовать что-то иное. То формулу полной вероятности, то классическое определение, то плотности интегрировать, то площади друг на друга делить, то свойства вероятностей использовать etc etc.



