infantier писал(а):
Решим эту систему рекурсивно, а именно последовательно вычислить значение каждого

,

, как отношение двух полиномов от

,

и

по формуле:

причем по индукции легко доказать, что для

выполняется неравенство:

. Откуда в частности следует, что никакой

не равен тождественно нулю (как функция от

,

,

).
Понятно, что выбрав какие-то числовые значения для

,

,

, мы получим решение тогда и только тогда, когда полином

не обращается в ноль. Поэтому достаточно выбрать
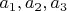
так, чтобы они не обращали в ноль

, а это для полинома не равного тождественному нулю всегда можно сделать (докажите в качестве несложного упражнения).