Посмотрите на функции из множества

- у них максимум в единице. У выпуклых комбинаций максимум там же и он строго больше единицы.
Далее от противного - пусть такая

найдется. Тогда ее очень хорошо приближает какая-то выпуклая комбинация. В частности в единице. Это значит что у

максимум в единице и в этой выпуклой комбинации участвуют элементы из

с большими номерами. У этих элементов с большими номерами очень близкое к нулю значение на полуинтервале
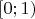
, значит

на этом полуинтервале тоже близка к нулю. Но максимум у нее в точке

и сколь угодно малое значение на полуинтервале
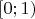
. Но такого не может быть из соображений непрерывности.