Задача 10.
Последовательность

, состоящую из натуральных чисел, можно рассматривать как отображение

(

--- множество натуральных чисел).
Для трех таких последовательностей

,

и

выполняются следующие условия: отображение

--- сюръективно, отображение

--- инъективно,

. Доказать, что

для всех

.
Это довольно очевидно, если считать

монотонной: поскольку она подпирает

снизу, у последней в множестве значений никак не может не оказаться пропусков (если

вплоть до
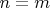
и

, то среди значений

уже заведомо не окажется

). Ну а монотонности

всегда можно добиться одновременной перестановкой обеих последовательностей.
Задача 8.
Рассматриваются матрицы, состоящие из пяти строк и восьми столбцов, все строки которых попарно различны. Доказать, что во всякой такой матрице можно указать четыре столбца, при вычеркивании которых строки получившейся матрицы также будут попарно различны. Показать, что пять таких столбцов можно указать не всегда.
Контрпример очевиден -- это единичная матрица. Надо доказать, что если

строк попарно различны, то они попарно различны не менее чем по

столбцу. Ну так по индукции же. Для

утверждение тривиально. Пусть оно верно для некоторого

. Для

попарно различных строк выберем

столбец, по которым попарно различны первые

строк. Последняя строка по этим столбцам если и совпадает, то разве что с одной из предыдущих строк. Но по хотя бы одному из оставшихся столбцов она от этой строки всё-таки отличается; вот этот столбец и добавим.



