Вероятность разбиения

[2old]

Случайным образом строим разбиение $(A_1,A_2,A_3)$ множества из $n = 9k$ элементов на три непересекающиеся равные части: $|A_i|=\frac{n}{3}=3k$, $|A_i\cap A_j| = 0$, $i\neq j$
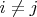
Разбиения считаются одинаковыми, если они состоят из одинаковых множеств, записанных в разном порядке. Например, $(A_1,A_2,A_3)=(A_2,A_1,A_3)$.
Пусть, кроме того, изначально в том же множестве из $n$ элементов было фиксировано подмножество $B$, $|B| = \frac{n}{3}=3k$ . Найдите $P(|B \cap A_i| = \frac{n}{9}, i = 1, 2, 3)$.

Подсчитаем общее число разбиений.
число способов выбрать элементы для $A_1$: $\binom{9k}{3k}$
число способов выбрать элементы для $A_2$: $\binom{6k}{3k}$
число способов выбрать элементы для $A_3$: $1$

Кроме того, нас не интересует порядок, поэтому общее число: $\frac{1}{3!}\binom{9k}{3k}\binom{9k}{3k}$

Число разбиений, при котором каждое из $A_i$ пересекается с $B$ по $k$ элементам
число способов выбрать элементы для $A_1$: $\binom{3k}{k}\binom{6k}{2k}$
число способов выбрать элементы для $A_2$: $\binom{2k}{k}\binom{4k}{2k}$
число способов выбрать элементы для $A_3$: $1$

Итого: $\frac{1}{3!}\binom{3k}{k}\binom{6k}{2k}\binom{2k}{k}\binom{4k}{2k}$

Искомая вероятность:

$$ P(|B \cap A_i| = \frac{n}{9}, i = 1, 2, 3)=\frac{\binom{3k}{k}\binom{6k}{2k}\binom{2k}{k}\binom{4k}{2k}}{\binom{9k}{3k}\binom{6k}{3k}}= \frac{(\binom{3k}{k})^3}{\binom{9k}{3k}} $$

Верно ли получилось? Я не очень уверен в том, что правильно учел, то что нам порядок не важен

[2old]

Проверили работу, ответ неверный. Но я никак не могу сообразить в чем подвох, даже нового ничего нет чтобы дописать.

[provincialka]

Многабукав...

Вот, например, как можно обозначить разбиение на 3 группы? Назначим каждому элементу номер группы, то есть 1, 2 или 3. Получаем перестановку с повторениями $3k$ единиц, $3k$ двоек и $3k$ троек. Чтобы не учитывать порядок групп, надо поделить это число на $3!$.

Можно считать, что множество $B$ состоит из первых $3k$ элементов $A$.

-- 07.12.2015, 21:24 --

Общее число разбиений подсчитано верно, хотя и сложно. Только там опечатки.