Если порядок поля

простое число

то элементами поля являются вычеты по модулю

Но если порядок поля — не единичная степень простого

то всё не так просто. В этом случае ненулевые элементы поля представляются многочленами степени не больше

над полем

(то есть коэффициенты этих многочленов — суть вычеты по модулю

). Соответствия между элементами такого поля и числами нет. Но можно представлять элементы

-мерными векторами над полем

(пример такого представления для поля

дан в википедии по указанной ссылке).
Но нам числа и не нужны, ведь при построении множества

проверяется условие

где

— примитивный элемент нашего поля

То есть для
Примера 3 нужно проверять чтобы многочлен

принадлежал полю
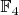
(точнее, подполю поля

изоморфному полю
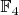
).



