Если немного ослабить условие: чтобы совпадали хотя бы "наборы цифр". Для маленьких чисел:

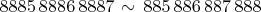
ну и так далее. А что, в раздел "Загадки" подошло бы.
Беда в том, что перестановками тут не получается равенства

То есть нужны другие соображения.
<Насчёт нормальности, намекнутой предыдущим оратором, чего-то не врубился

>.