Необыкновенно обыкновенное дифференциальное уравнение

[ProPupil]

Найти все решения дифференциального уравнения

$$y(y-1)+x(y\ln x + 1)y'+(x\ln x)^2(y')^2=0$$

[TripleLucker]

Попробовал преобразовать, может, поможет (дальше решить у меня тоже не выходит).
$\[\begin{array}{l} {y^2} + xyy'\ln x + xy' - y + {x^2}{\ln ^2}x{(y')^2} = 0\\ {(\frac{y}{x})^2} + \frac{y}{x}y'\ln x + (\frac{y}{x})' + {(y'\ln x)^2} = 0 \end{array}\]$ (тут я поделил на ${x^2}$)

Далее заменяем $y'\ln x = (y\ln x)' - \frac{y}{x}$ второй и четвертый член уравнения и получаем:

$\[(\frac{y}{x})' + {(\frac{y}{x})^2} + {((y\ln x)')^2} - \frac{y}{x}(y\ln x)' = 0\]$

Тут только два вида функций : $\frac{y}{x}$ и $y\ln x$, поэтому хотя бы выглядит приятнее.

[ProPupil]

Виноват, надо было домой придти и отослать, а не с рабочего места. В условии опечатка: во втором слагаемом перед скобкой ещё множитель 2 должен быть.

Т. е. уравнение имеет вид $y(y-1)+2x(y\ln x + 1)y'+(x\ln x)^2(y')^2=0$

[ProPupil]

Решение:

Домножаем левую и правую части уравнения на $x^{y-2}$.

В результате получаем уравнение

$y(y-1)x^{y-2} + 2x^{y-1}(y\ln x + 1)y' + x^y \ln x^2 (y')^2 = 0$. Домножением на $dx^2$ убеждаемся, что это уравнение эквивалентно

$d^2(x^y)=0$, что в свою очередь равносильно $d(x^y)=C_1dx + C_2dy.

Иными словами, мы имеем систему $yx^{y-1}=C_1, x^y\ln x = C_2$, дальше действуем в зависимости от констант $C_1, C_2$.

I. $C1 \ne 0, C2 \ne 0$
Делим второе на первое и получаем $\frac{x}{y}\ln x = C$ - одно решение
II. $C_1 \ne 0, C2 = 0$ - решений не даёт, поскольку ищем функцию $y=y(x)$
III. $C_1 = 0. C2 \ne 0$ - первое даёт $y=0$, что вступает в противоречие со вторым - решений не даёт.
IV. $C_1 = 0, C2 = 0$ - $y=0$, а также $x^y=C$, поскольку $d(x^y)=0$ тогда.

Ответ: $y = 0, x^y = C, \frac{x}{y}\ln x = C$ - все решения этого уравнения

[Null]

$x^y=c_1x+c_2$ наверно.

[M-1000]

Мне кажется, при взятии второй производной от х^y, слагаемое, содержащее вторую производную у, было упущено.

[ProPupil]

По какой переменной? По $y$?

$\left(x^y\right)''_{yy} = \left(x^y\ln x\right)'_y = x^y\ln^2 x$

Второй дифференцал: $d^2(x^y) = \dots dx^2 + \dots dxdy + x^y\ln^2 xdy^2$

При делении на $dx^2$ мы получаем $\frac{dy^2}{dx^2}$, а не $\frac{d^2y}{dx^2}$, так что всё верно.

[M-1000]

Прошу прощения за задержку с ответом.
Я выписывал второй дифференциал $x^y$ и у меня всегда появляется второй дифференциал $y$. Возможно, я напрочь утратил квалификацию со времен института. Вас не затруднит продемонстрировать выкладки?

[ProPupil]

Так сейчас сессия, понятное дело

Расписываю:

$\frac{\partial (x^y)}{\partial x}=yx^{y-1}$

$\frac{\partial (x^y)}{\partial y} = x^y\ln x$

$\frac{\partial^2 (x^y)}{\partial x^2} = \frac{\partial (yx^{y-1})}{\partial x} = y(y-1)x^{y-2}$

$\frac{\partial^2 (x^y)}{\partial x\partial y} = \frac{\partial (x^y \ln x)}{\partial x} = yx^{y-1}\ln x + x^y\cdot\frac{1}{x} = (1+y\ln x)x^{y-1}$

$\frac{\partial^2 (x^y)}{\partial x\partial y}=\frac{\partial (yx^{y-1})}{\partial y}=x^{y-1}+yx^{y-1}\ln x= (1+y\ln x)x^{y-1}$

Здесь я специально посчитал два раза: хотя для большинства функций смешанные производные и равны, осторожность никогда не повредит.

$\frac{\partial^2 (x^y)}{\partial y^2} = \frac{\partial(x^y\ln x)}{\partial y}=x^y\ln^2 x$

Далее, по формуле $d^2f = f''_{xx}dx^2+(f''_{xy}+f''_{yx})dxdy + f''_{yy}dy^2$

Отсюда и получаем

$$d^2(x^y) = y(y-1)x^{y-2}\,dx^2 = (1+y\ln x)x^{y-1}\,dx\,dy + x^y\ln^2 x\,dy^2$$

Если мы поделим это выражение на $dx^2$, то получим в соответствующих слагаемых:
$\frac{dx}{dx} = 1$

$\frac{dx\,dy}{dx^2}=\frac{dy}{dx}=y'$

$\frac{dy^2}{dx^2} = \frac{dy}{dx} \frac{dy}{dx} = (y')^2$

[M-1000]

Спасибо за ответ.
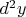
Я понимаю ваш подход. Вы берете выражение $x^y$ как функцию двух независимых переменных и находите её второй дифференциал. Но мне кажется в данном случае считать $y$ независимой переменной, а затем делить её дифференциал на дифференциал $x$ (получая производную $y'$) не следует. Если вы используете функцию двух переменных, то при таком подходе $d^2y$ у вас естественным образом должен быть равным нулю и вторая производная $y''$ уже не может появиться (не говоря о том, что тогда и $dy/dx$ должна быть равна нулю).
Думаю, правильно брать производную (или, если вам удобней, дифференциал) сложной функции. У меня получается:
$ f'=(e^{ylnx})'=e^{ylnx}(ylnx)'=e^{ylnx}(y'lnx+y/x)\\ f''=(x^y)'(y'lnx+y/x)+x^y(y'lnx+y/x)'=\\ =x^y(y'lnx+y/x)^2+x^y(y''lnx+2y'/x-y/x^2) $
Раскрывая скобки и вынося $x^{y-2}$, получаем:
$f''= x^{y-2}[(xlnx)^2(y')^2+2(xlnx)y\cdot y'+y^2+x^2lnx\cdot y''+2xy'-y]=\\ = x^{y-2}([y^2-y+2x(y\cdot lnx+1)y'+(xlnx)^2(y')^2]+x^2lnx\cdot y'')$
Выражение внутри квадратных скобок и есть ваше уравнение, которое таким образом отличается от второй производной $x^y$ не только множителем, но и наличием добавочного слагаемого, содержащего $y''$.

[ProPupil]

Идея здесь заключалась именно в обобщении метода полных дифференциалов.

Когда у нас есть уравнение вида

$$M(x,y)dx + N(x,y)dy = 0$$

, где $\exists f(x,y): f'_x=M(x,y) \text{ и } f'_y = N(x,y)$, то мы решаем это именно как $df=0$, или $f = C$.

Здесь я использовал тот же самый подход.

[VanD]

ProPupil в сообщении #1078766 писал(а):

$y(y-1)x^{y-2} + 2x^{y-1}(y\ln x + 1)y' + x^y \ln x^2 (y')^2 = 0$. Домножением на $dx^2$ убеждаемся, что это уравнение эквивалентно

$d^2(x^y)=0$, что в свою очередь равносильно $d(x^y)=C_1dx + C_2dy$.

Очень интересно.
Вы бы наверно уравнение $2x(y')^2 + 4yy' = 0$ решали так:
домножим на $dx^2$, получим $2x dy^2 + 4y dxdy = 0$. То есть $d^2 (xy^2) = 0$, то есть $d (xy^2) = C_1 dx + C_2 dy$, то есть $y^2 = C_1, 2xy = C_2$, как дальше?

ProPupil в сообщении #1085542 писал(а):

Идея здесь заключалась именно в обобщении метода полных дифференциалов.

Метод полных дифференциалов не с потолка берётся, там есть строгое обоснование таких трюков.

[DeBill]

Это шутка такая, да?
Оба решения, конечно, не подходят.
И не могут подходить, т.к. уравнение нелинейно, а предъявлнро ...