Гармонический анализ

[Asalex]

Уважаемые форумчане!

Имеется функция $\chi(\xi)\inC^{\infty}(\mathbb{R})$ такая что $\mbox{supp} \chi\subset(-2,-\frac12)\cup(\frac12,2),$ и для всякого $\xi\neq0$

$$\sum\limits_{j=-\infty}^{+\infty}\chi\left(\frac{\xi}{2^j}\right)=1.$$

(Легко понять, что такие функции существуют, достаточно задать её на интервале $\left(\frac{1}{2},1\right)$ так что $\chi\left(\frac12\right)=0,$ $\chi\left(1\right)=1,$ и все производные $\chi^{(j)}\left(\frac12\right)=\chi^{(j)}\left(1\right)=0,$ $j=1,2,3,\dots.$)

Тогда для любой функции в фазовом пространстве $f(x)\in L_2(\mathbb{R}_x)$ можно определить проектор

$$f_j(x)\equiv P_j f(x) = \mathfrak{F}^{-1}\left[\psi\left(\frac{\xi}{2^j}\right)\hat f(\xi)\right],\qquad \hat f(\xi):=\mathfrak{F}[f](\xi),\quad \hat f_j(\xi):=\psi\left(\frac{\xi}{2^j}\right)\hat f(\xi),$$

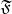
где $\mathfrak{F}$- преобразование Фурье. (То есть грубо говоря $P_j f(x)$ - это та часть функции $f(x)$, которая отвечает за гармоники, попадаюшие в интервал $(2^{j-1},2^{j+1})$).

Легко видеть, что $P_j$ и оператор дифференцирования по $x$ перестановочны. Тогда для производных имеем:

$$\mathfrak{F}^{-1}\left[P_jf'(x)\right] = i\xi\psi\left(\frac{\xi}{2^j}\right)\hat f(\xi),\hskip11cm(1)$$

и поскольку носитель функции $\psi\left(\frac{\xi}{2^j}\right)$ сосредоточен в интервале $(2^{j-1},2^{j+1})$, то в силу равенства Парсеваля для $L_2$ нормы имеем:

$$\left\|f'_j(x)\right\|_{L_2(\mathbb{R}_x)}=\left\|\mathfrak{F}^{-1}f'_j(x)\right\|_{L_2(\mathbb{R}_{\xi})} = \left\|i\xi\psi\left(\frac{\xi}{2^j}\right)\hat f(\xi)\right\|_{L_2(\mathbb{R}_{\xi})}\sim 2^j\left\|\psi\left(\frac{\xi}{2^j}\right)\hat f(\xi)\right\|_{L_2} = 2^j\left\|\hat f_j(\xi)\right\|_{L_2}. \hskip6mm(2)$$

Вопрос: справедливо ли аналогичное равенство для нормы,

$$\left\|f'_j(x)\right\|_{L_{\infty}(\mathbb{R}_x)}=2^j\left\|\hat f_j(\xi)\right\|_{L_2}?\hskip11cm(3)$$

[Red_Herring]

(2): Для "одного порядка величины" используется знак $\asymp$ а никак не $\sim$

(3) Какая норма д.б. справа? Какой знак между ними

[Asalex]

Прошу прощения, неправильно написал что меня интересует.
Для $L_2$ мы имеем:

$$\left\|\partial_x f\right\|_{L_2}\asymp 2^j\left\|f\right\|_{L_2} \quad \textrm{при}\quad j\to\infty\hskip5cm (2b)$$

Выполняется ли это так же для равномерной нормы, то есть верно ли что

$$\left\|\partial_x f\right\|_{L_{\infty}}\asymp 2^j\left\|f\right\|_{L_{\infty}}.\hskip72mm(3b)?$$

[Red_Herring]

Ваш оператор — это свёртка с некоторой функцией. Какой?

В 50е была статья Хёрмандера переведённая на русский в виде брошюры "Библиотека сборника «Математика»": Операторы инвариантные относительно сдвига". Стоит посмотреть и там

[Asalex]

Преобразование Фурье от моего оператора, это
$\mathfrak{F}[P_jf](\xi)=\psi\left(\frac{\xi}{2^j}\right) * \widehat{f} (\xi)=\int\limits_{-\infty}^{+\infty}\psi\left(\frac{\xi-\eta}{2^j}\right)\widehat{f}(\eta)d\eta.$

[Vince Diesel]

Для целых функций конечного порядка (которыми являются $f_j$) и их производных есть неравенство Бернштейна, а для разных метрик $L_p$ — неравенство Никольского. Так что с какими-то константами оценку для $\partial_xf_j$ получить можно. От чего они зависят, надо проверять.

[Red_Herring]

Можно так, а можно в терминах оригиналов, а не преобразований Фурье $f$ и $P_jf$ но тогда будет п.Ф. от $\psi_j$. Вам же нужны $L^p $ нормы оригиналов