Это зависит от читателя. Я, например, не пользуюсь знаками интеграла, указывающими на замкнутость кривой или поверхности, вне зависимости от ее размерности. Вообще никогда, даже на письме и для аудитории.
Все, завязываем с оффтопом, плиз. Это не сюда.
Смысл такого обозначения - не в том, чтобы указать на замкнутость, а в том, чтобы указать на контурность. То есть, если присутствуют, скажем, два интеграла, по

и по
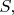
то знак контурного интеграла указывает на то, что данная

есть поверхность данной

Если хотите - отделите. Я тоже думаю, что не сюда, но прорвало.
-- 12.11.2015 21:49:23 --А чему это равно по формуле Гаусса-Остроградского, и какие у нее условия применимости?
Плюс какие условия применимости у равенства под знаком интеграла.