О задании структуры на произвольном X

[Dmitry Tkachenko]

Сначала расскажу задачу, а в конце --- зачем это нужно.

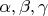
Задача. Пусть задано некоторое множество $X$. Три произвольных семейства $\{U_{\alpha}\}, \{V_{\beta}\}, \{W_{\gamma}\}$ подмножеств $X$ таковы, что множества каждого из них покрывают $X$ ($\alpha, \beta, \gamma$ из одного индексируещего множества $T$). Рассмотри три множества обратимых отображений на $\mathbb{R}^n$: $\mathcal{A} =\{\varphi_{\alpha} \colon U_{\alpha} \to \mathbb{R}^n\}, \mathcal{B}=\{\psi_{\beta} \colon V_{\beta} \to \mathbb{R}^n\}, \mathcal{C}=\{\theta_{\gamma} \colon W_{\gamma} \to \mathbb{R}^n\}.$ Известно, что
1) $\varphi_{\alpha}(U_{\alpha} \cap V_{\beta}), \psi_{\beta}(U_{\alpha} \cap V_{\beta})$ и $\psi_{\beta}(V_{\beta} \cap W_{\gamma}), \theta_{\gamma}(V_{\beta} \cap W_{\gamma})$ открыты в $\mathbb{R}^n;$
2) взаимнообратные отображения

$\psi_{\beta}(\varphi^{-1}_{\alpha}) \colon \varphi_{\alpha}(U_{\alpha} \cap V_{\beta}) \to \psi_{\beta}(U_{\alpha} \cap V_{\beta}),$
$\varphi_{\alpha}(\psi^{-1}_{\beta}) \colon \psi_{\beta}(U_{\alpha} \cap V_{\beta}) \to \varphi_{\alpha}(U_{\alpha} \cap V_{\beta})$

и

$\theta_{\gamma}(\psi^{-1}_{\beta}) \colon \psi_{\beta}(V_{\beta} \cap W_{\gamma}) \to \theta_{\gamma}(V_{\beta} \cap W_{\gamma}),$
$\psi_{\beta}(\theta^{-1}_{\gamma}) \colon \theta_{\gamma}(V_{\beta} \cap W_{\gamma}) \to \psi_{\beta}(V_{\beta} \cap W_{\gamma})$

являются гомеоморфизмами.

Правда ли, что
(i) $\varphi_{\alpha}(U_{\alpha} \cap W_{\gamma}), \theta_{\gamma}(U_{\alpha} \cap W_{\gamma})$ открыты в $\mathbb{R}^n;$
(ii) взаимнообратные отображения

$\varphi_{\alpha}(\theta^{-1}_{\gamma}) \colon \theta_{\gamma}(U_{\alpha} \cap W_{\gamma}) \to \varphi_{\alpha}(U_{\alpha} \cap W_{\gamma}),$
$\theta_{\gamma}(\varphi^{-1}_{\alpha}) \colon \varphi_{\alpha}(U_{\alpha} \cap W_{\gamma}) \to \theta_{\gamma}(U_{\alpha} \cap W_{\gamma})$

являются гомеоморфизмами?

Зачем это нужно.
A) Если это правда, то мы получим отношение эквивалентности для $\mathcal{A}, \mathcal{B}, \mathcal{C}$.

B) Если d1) отображения $\varphi, \psi, \theta$ называть $n$-мерными картами,

d2) условия 1) и 2) --- $\mathcal{C}^0$-согласованностью $\varphi, \psi$ и $\psi, \theta$ соответственно,

d3) совокупности карт $\mathcal{A}, \mathcal{B}, \mathcal{C}$ --- $n$-мерными $\mathcal{C}^0$-атласами, то

отношение эквивалентности разбивает множество $n$-мерных $\mathcal{C}^0$-атласов на непересекающиеся классы, которые называют $n$-мерными $\mathcal{C}^0$-структурами. А значит, произвольное $X$ можно наделить $n$-мерной $\mathcal{C}^0$-структурой.

[Dmitry Tkachenko]

Dmitry Tkachenko в сообщении #1065633 писал(а):

отображений на $\mathbb{R}^n$

Я прошу прощения. Все эти биекции на открытые подмножества $\mathbb{R}^n.$ Или даже на открытые подмножества произвольного конечномерного или бесконечномерного банахового пространства $\mathbb{B}.$

Нагуглил Бурбаки Н. "Аналитические и дифференцируемые многообразия", издательство "Мир", Москва, 1975. - 220 с. Там это пункты 5.1.1-5.1.3 и они говорят, что утверждение справедливо даже для $\mathbb{B}.$ Ссылок на доказательства не дают.