NP не равно P

[bilan]

NP не равно P.
авторы: Виталий Коваль, Игорь Билан.
Электронная почта: mathbilan [at] gmail [dot] com.
Целью данного сообщения является доказательство того факта что NP не равно P.
Определение 0.1: граф $G$ это неориентированый граф из $n$ вершин.
Определение 0.2: максимальная клика графа $G$ это клика $C$ из $2\log_2n$ вершин. В нашем случае $2\log_2n$ вершин выбираются случайным образом и достраиваются до рёбер клики.
Определение 0.3:$V(G)$ это множество вершин графа $ G $.
Определение 0.4:$V(C)$ это множество вершин клики $ C $.
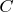
Определение 0.5:$V(F)$ это множество вершин клики $ F $.
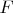
Лемма 0.6. В типичном случае граф $ G $ содержит клику $F$ из $d$ вершин если $2(\log_2n-\log_2\log_2n)-1<d<2(\log_2n-\log_2\log_2n)+4$. И в типичном случае если $2(\log_2n)>d>2(\log_2n-\log_2\log_2n)+4$ то $F \in C$ . И в типичном случае если $2(\log_2n)<d$ то $F \notin G$ .


Доказательство: В типичном случае граф из $ V(G)\setminus V(C) $ вершин содержит клику из $d$ вершин если $2(\log_2n-\log_2\log_2n)-1<d<2(\log_2n-\log_2\log_2n)+4$ согласно [1].
И если математическое ожидание числа клик равно $ \binom{n}{r}2^{-\binom{r}{2}}$
то $ r = |V(F)|$ мы получаем , если $ |V(F)\cap V(C)|\sim k $ и $k$ мало мы получаем
математическое ожидание числа клик равно $ \binom{n}{r-k}2^{-\binom{r-k}{2}}\binom{2\log_2 n}{k}2^{-(r-k)k}\to 0$.

Если $ |V(F)\cap V(C)|\sim k $ и $k\sim \log_2n$ то мы имеем
математическое ожидание числа клик равно $ \binom{n}{r-k}2^{-\binom{r-k}{2}}\binom{2\log_2 n}{k}2^{-(r-k)k}\to 0$.
Если $ |V(F)\cap V(C)|\sim k $ и $k\sim 2 \log_2n$ то мы имеем
математическое ожидание числа клик равно $ \binom{n}{r-k}2^{-\binom{r-k}{2}}\binom{2\log_2 n}{k}2^{-k2\log_2n}\to 0$.
Конец доказательства леммы.
Определение 0.7:
Случайная величина суть $ X $.
Дисперсия $X$ суть $D(X)$.
Сигнал суть $S$.
Математическое ожидание $X$ суть $E(X)$.
Функция плотности вероятности $X$ суть $f(x)$.
Лемма 0.8
В типичном случае если число испытаний мало и $S=o(\sqrt{D(X)})$ и $f(x)\nearrow \colon x< E(X)$ и $f(x)\searrow \colon x> E(X)$ то мы не можем зафиксировать сигнал $S$.
Доказательство:
Доказательство предоставляется читателю.
Конец доказательства леммы.

Определение 0.9:
$H^1(G)$ это множество рёбер графа $G$.
Определение 0.10:
$T$ это число операций алгоритмической машины.
$T=n^m<n^{\log_2\log_2n}$
Определение 0.11:
$v \in V(G)$;
$H_1(v)=\{\eta \colon (v,\eta)\in H^1(G)\}$.
Лемма 0.12
$\eta_1 \in H_1(v)$ ;
$\eta_2 \in (H_1(v)\cap H_1(\eta_1))$;
$\eta_3 \in (H_1(v)\cap H_1(\eta_1)\cap H_1(\eta_2))$;
$\eta_4 \in (H_1(v)\cap H_1(\eta_1)\cap H_1(\eta_2)\cap H_1(\eta_3))\ldots$;
$\eta_i \in (H_1(v)\cap H_1(\eta_1)\cap H_1(\eta_2)\ldots \cap H_1(\eta_{i-1}))$;
мы имеем если $i<\log_2n/2$ то $T>n^{\log_2n/2}$. И $S=o(\sqrt{D(X)})$ применяя мемму 0.8
Доказательство леммы:
Если $X=|(H_1(v)\cap H_1(\eta_1)\cap H_1(\eta_2)\ldots \cap H_1(\eta_{i-1}))|$ и $S=2\log_2n$ то $S=o(\sqrt{D(X)})$; если $i<\log_2n/2$ то $X\sim n/2^{\log_2n/2}\sim \sqrt{n}$ и $D(X)\sim pq\sqrt{\sqrt{X}} ;q=p=1/2$ $\Rightarrow$ $S=o(\sqrt{D(X)})$. Применяем мемму 0.8. Согласно [1] то мы имеем в графе из $(H_1(v)\cap H_1(\eta_1)\cap H_1(\eta_2)\ldots \cap H_1(\eta_{i-1})) \sim \sqrt{n}$ вершин в типичном случае содержит клику $F$ и $V(F)\sim 2(\log_2\sqrt{n}-\log_2\log_2\sqrt{n})-1$. Мы имеем вершины $C$ в $\sqrt{n}$ вершин и $T=n^{\log_2\log_2n}$ $\Rightarrow$ $(2\log_2n/n)^{a}\sqrt{n}^aT$ $S=a$ $\Rightarrow$ $a=2\log_2\log_2n$. То мы не можем зафиксировать сигнал $S$.
Конец доказательства.
Определение 0.13:
Граф $ G_1 $ это неориентированный граф.
$V(G_1)=\{$клики из $\log_2\log_2n$ вершины графа $G \}$.
$(\alpha_{b_1},\beta_{b_2})$ это ребра $G_1$ если в $G$ клики $\alpha_{b_1},\beta_{b_2}$ соединены рёбрами если $\Rightarrow$
(1) Если $\alpha_{b_1},\beta_{b_2}\in G_1 $ и $V(\alpha_{b_1})\cap V(\beta_{b_2})=\emptyset$ и $\forall v_1 \in V(\alpha_{b_1})$ и $\forall v_1 \in V(\beta_{b_2})$ $\Rightarrow$ $ (v_1,v_2) \in H^1(G) $ то $D(X)$ минимальна.
(2) Если $\alpha_{b_1},\beta_{b_2}\in G_1 $ и $\forall v_1 \in V(\alpha_{b_1})$ и $\forall v_1 \in V(\beta_{b_2})$ $\Rightarrow$ $ (v_1,v_2) \in H^1(G) $ то $D(X)$ больше.
(3) Если $\alpha_{b_1},\beta_{b_2}\in G_1 $ и $\exists v_1 \in V(\alpha_{b_1})$ и $\exists v_1 \in V(\beta_{b_2})$ $\Rightarrow$ $ (v_1,v_2) \in H^1(G) $ то $D(X)$ больше.
Лемма 0.14
В лемме 0.12 аналогично заменяем $G$ на $G_1$ и мы также не можем зафиксировать сигнал $S$.
Доказательство:
Доказательство предоставляется читателю.
Конец доказательства леммы.


Рис.1 матрица смежности с $Y_1,Y_2,Y_3$


Рис.2 матрица смежности с $Y$ и $u$



Определение 0.15:
$Y \subseteq V(G)*V(G)$.
$Y^1=|\{Y\cap H^1(G) \}|$.
Лемма 0.16
Расположение $Y_1,Y_2,Y_3$ показано на Рис.1. $Y_3\subseteq Y_2$.
Если $Y^1_1>Y^1_3 $ то заменим $Y_1$ на $Y_3$ в $Y_2$. Если $|V(Y_1)|<\sqrt{n}$ мы не можем зафиксировать сигнал $S$.

Доказательство:
Доказательство предоставляется читателю.
Конец доказательства леммы.

Лемма 0.17
Расположение $Y_1,Y_2,Y_3$ показано на Рис.1. $Y_3\subseteq Y_2$.
Если $Y^1_1>Y^1_3 $ то заменим $Y_1$ на $Y_3$ в $Y_2$. Если $\sqrt{n}<|V(Y_1)|<n/5$ мы не можем зафиксировать сигнал $S$.

Доказательство:
Доказательство предоставляется читателю.
Конец доказательства леммы.

Лемма 0.18
Расположение $Y_1,Y_2,Y_3$ показано на Рис.1. $Y_3\subseteq Y_2$.
Если $Y^1_1>Y^1_3 $ то заменим $Y_1$ на $Y_3$ в $Y_2$. Если $|V(Y_1)| \sim n$ мы не можем зафиксировать сигнал $S$.

Доказательство:
Доказательство предоставляется читателю.
Конец доказательства леммы.

Лемма 0.19
Расположение $Y$ показано на Рис.2. $Z_1\subseteq V(G)$ и $Z_2\subseteq V(G)$ и $|Z_1|=|Z_2|$.
Если $Y^1(Z_1)>Y^1(Z_2) $ то заменим $Z_1$ на $Z_2$ в $Y$. Если $u \sim n$ мы не можем зафиксировать сигнал $S$. Если $\sqrt{n}<u<n/5$ мы не можем зафиксировать сигнал $S$. Если $u<\sqrt{n}$ мы не можем зафиксировать сигнал $S$.
Доказательство:
Доказательство предоставляется читателю.
Конец доказательства леммы.
Лемма 0.20
В лемме 0.19 аналогично заменяем $G$ на $G_1$ и мы также не можем зафиксировать сигнал $S$.
Доказательство:
Доказательство предоставляется читателю.
Конец доказательства леммы.

Лемма 0.21
В лемме 0.16, лемме 0.17, лемме 0.18, аналогично заменяем $G$ на $G_1$ мы также не можем зафиксировать сигнал $S$.

Доказательство:
Доказательство предоставляется читателю.
Конец доказательства леммы.

Определение 0.22
Граф $ G_3 $ это граф $ G $ с переименованными вершинами.


Лемма 0.23
Шаг 1. $Z_1\subseteq V(G_3)$ и $Z_2\subseteq V(G_3)$ и $|Z_1|=|Z_2|$ и $Z_1,Z_2$ пробегает $V(G_3)$
Шаг 2. Меняя местами $Z_1$ и $Z_2$ в графе $G_3$ получаем $G^1_3$
Шаг 3. Если $|H^1(G)\cap H^1(G_3)|<|H^1(G)\cap H^1(G^1_3)|$ то $G_3:=G^1_3$.
Шаг 4. Переходим к шагу 1.
Мы также не можем зафиксировать сигнал $S$.
Доказательство:
$D(X) \sim (n/2)pq; p=q=1/2$. $S=2\log_2n$. $S=o(\sqrt{D(X)})$. Используем лемму 0.8.
Конец доказательства леммы.

Лемма 0.24
В лемме 0.23, аналогично заменяем $G$ на $G_1$ то мы также не можем зафиксировать сигнал $S$.
Доказательство:
Доказательство предоставляется читателю.
Конец доказательства леммы.
Определение 0.25:
Граф $ G_2 $ это неориентированный граф и $G_2 \ne G $
Лемма 0.26
Шаг 1. $Z_1\subseteq V(G_2)$ и $Z_2\subseteq V(G_2)$ и $|Z_1|=|Z_2|$ и $Z_1,Z_2$ пробегает $V(G_2)$
Шаг 2. Меняя местами $Z_1$ и $Z_2$ в графе $G_2$ получаем $G^1_2$
Шаг 3. Если $|H^1(G)\cap H^1(G_2)|<|H^1(G)\cap H^1(G^1_2)|$ то $G_2:=G^1_2$.
Шаг 4. Переходим к шагу 1.
Мы также не можем зафиксировать сигнал $S$.
Доказательство:
Если $|H^1(G)\cap H^1(G_2)\cap (V(G)*Z_i)|<\sqrt{n}$ то $S=o(\sqrt{D(X)})$.
Если $|H^1(G)\cap H^1(G_2)\cap (V(G)*Z_i)|>\sqrt{n}$ то $S=o(\sqrt{D(X)})$.
Если $|H^1(G)\cap H^1(G_2)\cap (V(G)*Z_i)|\sim n$ то $S=o(\sqrt{D(X)})$.
Используем лемму 0.8.
Лемма 0.27
В лемме 0.26,аналогично заменяем $G$ на $G_1$ то мы также не можем зафиксировать сигнал $S$.
Доказательство:
Доказательство предоставляется читателю.
Конец доказательства леммы.


Определение 0.28:
Алгоритмическая машина J это
(1) $Y_1, Y_2, \ldots ,Y_{n^m}$
(2)IF $Y_i>Y_j$ THEN $\ldots$
(3)$Y_w$ генерируется из $V(Y_i)$
(4)$V(Y_i)$ to $\cap \, \setminus \,\cup $
(5) $R_i$ переменные для промежуточных вычислений.
(6) $>\, <\, =\, IF\, R_i<R_j \, THEN \,\ldots $; $\,IF\, R_i>R_j \, THEN \,\ldots \,$; $\,IF\, R_i=R_j \, THEN \,\ldots \,$
(7) $ *\, , /\, , +\, , -\,$ on $R_i$.
Лемма 0.29
Алгоритмическая машина J полиномиально эквивалентна машине Тьюринга.
Доказательство:
Согласно [2], мы получаем $J \sim NARX$ нейронной сети, и мы получаем машина Тьюринга $\sim NARX$ нейронной сети.

Конец доказательства леммы.
Лемма 0.30
Если задаче поиска клики свести к другой NP-полной проблеме то при обратном переходе мы приходим к лемме 0.26.
Доказательство:
Доказательство предоставляется читателю.
Конец доказательства леммы.
Лемма 0.31
Если мы не ищем максимум $R_i$ то также не можем зафиксировать сигнал $S$.

Доказательство:
Доказательство предоставляется читателю.
Конец доказательства леммы.

Лемма 0.32
Если $T=\log_2\log_2n$ то мы можем зафиксировать $\log_2\log_2n$ вершин и сузить поиск до $\sqrt{n}$ вершин. Леммы остаются в силе.

Доказательство:
Доказательство предоставляется читателю.
Конец доказательства леммы.
Лемма 0.33
Мы можем использовать менее $T<n^{\log_2\log_2n}$ объектов $Y_l$.

Доказательство:
Доказательство предоставляется читателю.
Конец доказательства леммы.

Теорема 0.34
Используя леммы этой работы мы получаем, что NP не равно P.
Доказательство:
Доказательство предоставляется читателю.
Конец доказательства теоремы.




1.А.Д.Коршунова «Основные свойства случайных графов с большим числом вершин и рёбер» Успехи математических наук том 40 выпуск 1(241) 1985 год январь-февраль.
2. Саймон Хайкин Нейронные сети: полный курс 2-е издание Москва Санкт-Петербург Киев Вильямс 2006

[whitefox]

Зачем так многабукафф?
Можно куда проще, например:

Теорема 0.0
NP не равно P.
Доказательство:
Доказательство предоставляется читателю.
Конец доказательства теоремы.

[bilan]

статья около полугода проходила рецензирование в трудах американского математического общества и теперь ее статус следующий:
Article Status: Reviewing
Your paper is being handled by an editor.
что это точно значит, не знаю, но может быть для кого то это будет полезно.
редактор --Sergei K Suslov

[Mihaylo]

bilan в сообщении #1064324 писал(а):

Article Status: Reviewing
Your paper is being handled by an editor.

Статус статьи: рассматривается
Твоя бумага обрабатывается редактором

[bot]

bilan в сообщении #1064324 писал(а):

Your paper is being handled by an editor

Редактор безуспешно ищет желающих отрецензировать.
Ваша статья обрабатывается редактором.

[m(Ax)]

Попытался прочитать . Споткнулся уже на определении 0.2. Обычно под максимальной кликой понимается клика которая не содержится ни в какой другой клике большего размера. Что же определяется здесь, от меня совершенно ускользает.
Далее, лемма 0.7. Что означает "в типичном случае"?
Определение 0.7. Хотелось бы все же определение, а не просто перечисление непонятно чего.
Ну и лемма 0.8, что означает "зафиксировать сигнал S"?

Учитывая, что практически во всех леммах мы "не можем зафиксировать сигнал", дальше пока читать не стал до прояснения .

[bilan]

определение 0.2 станет понятнее если проработать статью

bilan писал(а):

А.Д.Коршунова «Основные свойства случайных графов с большим числом вершин и рёбер» Успехи математических наук том 40 выпуск 1(241) 1985 год январь-февраль.

ответ на

m(Ax) писал(а):

Далее, лемма 0.7. Что означает "в типичном случае"?

содержится в той же статье А.Д.Коршунова
определение 0.7 это скорее соглашение об обозначениях
ответ на

m(Ax) писал(а):

Ну и лемма 0.8, что означает "зафиксировать сигнал S"?

в условиях леммы 0.8 мы не можем отличить $X+S$ и $X$ при одном испытании.

-- 26.10.2015, 13:06 --

точнее если число испытаний мало

[Deggial]

Тема перемещена из форума «Дискуссионные темы (М)» в форум «Карантин»
Причина переноса: не оформлены цитаты

bilan
Освойте тег quote, а также кнопки и , исправьте цитаты в последнем сообщении.
См. также тему Что такое карантин, и что нужно делать, чтобы там оказаться.
После исправлений сообщите в теме Сообщение в карантине исправлено, и тогда тема будет возвращена.

Тема перемещена из форума «Карантин» в форум «Дискуссионные темы (М)»
Возвращено

[bilan]

пришел ответ:

Dear Prof. Bilan,

This message concerns the manuscript

NP is not P
by Vitaliy Vladimirovich Koval and Igor Urevich Bilan

submitted to Proceedings of the AMS.

Unfortunately, we cannot accept it for publication. It does not meet the standards that we require. Most results are not proved anyway and the proofs are left to the reader.

We apologize for taking such a long time to make this decision. The editor originally in charge of your submission had health problems and was unable to perform his duties for PAMS.

Sincerely,

Walter Van Assche
Editor of Proceedings of the American Mathematical Society

[Sender]

Жалко редактора.

[bot]

Долго редактор думал, даже занемог, бедняга, но ответ дал толерантный.

[vicvolf]

bot в сообщении #1095219 писал(а):

Долго редактор думал, даже занемог, бедняга, но ответ дал толерантный.

Учитесь!

[Мастак]

bot в сообщении #1095219 писал(а):

Долго редактор думал, даже занемог, бедняга, но ответ дал толерантный.

долго оценивал и потом решил, что был болен, так как не мог так долго оценивать

и потом редактора осенило - "так и по формальным свойствам же доказательства нет" - что и ответил

-- Сб фев 06, 2016 15:12:05 --

то есть:
берется NP-полная (NP-трудная в более ... представлениях) задача "Существует ли клика данного размера в произвольном графе?" и делается попытка доказать, что
не существует полиномиального (по затрачиваемым ресурсам скорости и памяти) алгоритма, решающего это задачу, для чего оценивается математическое ожидание роста затрат вычислительных ресурсов в зависимости от роста "сложности" (оцениваемой числом вершин) задачи при работе некоторой абстрактной машины,
которая выполняет расчет по любому алгоритму, решающему задачу

Так?

[Lia]

Тема перемещена из форума «Дискуссионные темы (М)» в форум «Пургаторий (М)»
Будучи полностью солидарными с редактором, мы приносим свои извинения за столь долгое время, которое понадобилось на принятие настолько очевидного решения.