Вопрос к аудитории: можно ли провести доказательство экспоненциальной сложности задачи следующим образом?
Определение. Задача экспоненциально сложна, если она полиномиально сводится к двум и более
различным задачам того же класса эквивалентности, но меньшей размерности, при этом не сводится полиномиально к одной такой задаче.
Рассмотрим задачу выполнимости булевых формул SAT (ВЫП). Допустим булевы формулы представляют собой

дизъюнкций и включают в себя

булевых переменных

. Рассмотрим произвольную булеву переменную

. Переменная

может не присутствовать в

дизъюнкциях, в

дизъюнкциях эта переменная может присутствовать без отрицания и в

дизъюнкциях - может присутствовать с отрицанием. При этом

.
Рассмотрим
задачу №1 меньшей размерности

. При подстановке значения

во все булевы формулы выполняются

дизъюнкций, остается определить выполнимость остальных

дизъюнкций. При этом заметим, в худшем случае количество дизъюнкций может оказаться тем же, что у исходной задачи (при

).
Задача №2 размерности

получается подстановкой
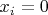
во все булевы формулы. В таком случае выполняются совершенно другие

дизъюнкций, аналогичным образом остается определить выполнимость остальных

дизъюнкций.
Можно свести задачи №1 и №2 к более простым подзадачам, у которых отсутствуют общие

дизъюнкций. Очевидно, что такие задачи разные, так как имеют разные входные данные - разные

и

дизъюнкции. В то же время данные "простые" задачи принадлежат к тому же классу эквивалентности, что и исходная задача SAT, так как формулируются одинаково.
Задачу SAT нельзя полиномиально свести к одной из задач (№1 или №2), так как в случае определения невыполнимости одной из задач потребуется определить выполнимость другой задачи.
Можно также попытаться уменьшить размерность задачи не вдоль

, а вдоль

. Для этого необходимо избавиться от одной из дизъюнкций, предположив ее либо равной нулю, либо единице. Когда дизъюнкция равна нулю, все булевы переменные, входящие в нее, должны быть равными нулю. Когда дизъюнкция равна единице, тогда хотя бы одна из переменных должна быть равной единице. Видно, что здесь можно повторить те же рассуждения, что и в случае присвоения нуля и единицы произвольной переменной

. Подзадачи, которые будут получены в ходе этих рассуждений, будут различными и будут принадлежать к классу эквивалентности задачи SAT.
Отсюда, по определению, задача SAT экспоненциально сложна, а значит

.




