Требуется решить уравнение

.
Очевидно, корни

и

, больше корней нет.
Надо доказать почему больше корней нет.
При
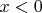
очевидно неравенство

, соответственно там корней нет.
Не очень понятно, что делать с промежутками

и

.
Пытался при помощи производной доказать, в т.ч. методом двух пешеходов и пр.
Можно рассмотреть функцию

То есть мысль какая: нужно показать, что при


, а при


или

.
Может быть есть мысли, как еще можно сделать или можно ли доделать методом с производной?