Они составляют базис эрмитовых матриц с нулевым следом именно в том смысле, что каждой из этих соответствует комбинация

, где

—
комплексные. Так что насчёт сложения всё прекрасно — хоть на

мы их умножай, хоть каждую на какое-то своё ненулевое комплексное число. Остаётся только умножение, и проще всего с ним разделаться, получив из новых матриц старые, что видно как.
Вместо матриц Паули можно рассматривать какой-то ортонормированный базис
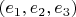
векторной части алгебры Клиффорда

, подалгебра

которой, где

, изоморфна

. Здесь выполняются схожие соотношения:

Из линейных комбинаций

с «комплексными» коэффициентами вида

мы получим все элементы алгебры. И, как действительно можно видеть, порождаемая уже

алгебра изоморфна

, но если мы не расстанемся с псевдоскаляром

, мы опять получим всю

целиком. Как-то так. Надеюсь, не сильно сумбурно.



