В учебниках по физике условия на разрыве выводятся обычно по-странному, мягко говоря. В то время как на самом деле эти условия являются прямым следствием определения обобщенного решения соответствующих уравнений движения. Отметим, попутно, что уравнения теории удара в классической механике также являются следствием определения обобщенного решения и выводятся совершенно аналогично условиям на разрыве в МСС.
Выведем условия на разрыве для стационарного уравнения Эйлера и уравнения неразрывности.
Рассмотрим область


В области

стационарно движется жидкость. Зпишем уравнение Эйлера и уравнение неразрывности:

где

-- частная производная вдоль

ой декартовой координаты

. По повторяющимся индексам суммирование. Массовая сила

является гладкой функцией.
В интегральной форме уравнения (*) приобретают вид


.
В отличие от уравнений (*), уравнения (**) позволяют рассматривать разрывные в

функции

, что и нужно в данной задаче.
Выполним преобразования, считая указанные функции гладкими в каждой из областей

.

интегрируем по частям:

где

-- компоненты вектора единичной внешней к

нормали, см картинку.
Аналогично,

И тоже самое с правой частью первого уравнения системы (**).
Возвращая полученные выражения обратно в интегральное уравнение, получаем

Индексом "+" будем помечать предельные значения функций на границе раздела областей со стороны области

, а индексом "-" со стороны области

.
В силу того, что пробные функции можно брать любыми, из последнего интегрального равенства следует, что на общем куске границе областей

верна формула

Рассуждая как и выше, из второго уравнения системы (**) находим

Это и есть условия на сильном разрыве.
Пример. [МСС в задачах, под редакцией М.Э. Эглит]

На крышу дома вертикально падает дождь плотности

, со скоростью при подлете

. Угол наклона крыши

. Считать процесс стационарным, скорость частиц ,стекающей по крыше жидкости постоянна. Найти положение границы, отделяющей воду от дождя. Атмосферное давление равно
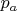
, плотность воды

.
Будем искать обобщенное решение с разрывом в форме прямой, которая отходит от вершины крыши, единичная нормаль к прямой

торчит вверх. Значит область

сверху, область

примыкает к крыше.
Введем декартову систему координат

с началом в вершине крыши, ось

смотрит вертикально вверх,


-- угол наклона разрыва к оси

.
В задаче три неизвестных:

. И три уравнения в рамке;
